The polarizace světla Jedná se o jev, ke kterému dochází, když elektromagnetická vlna, která tvoří viditelné světlo, osciluje v preferenčním směru. Elektromagnetická vlna se skládá z elektrické vlny a magnetické vlny, obě příčné ke směru šíření. Magnetická oscilace je simultánní a neoddělitelná od elektrické oscilace a probíhá ve vzájemně kolmých směrech..
Světlo, které vyzařuje většina světelných zdrojů, jako je Slunce nebo žárovka, je nepolarizované, což znamená, že obě složky: elektrická i magnetická, kmitají ve všech možných směrech, i když vždy kolmo ke směru šíření..
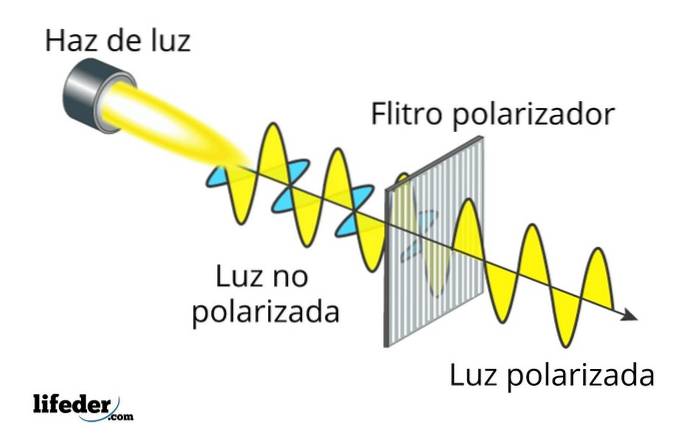
Pokud ale existuje preferenční nebo jedinečný směr oscilace elektrické komponenty, mluvíme o polarizované elektromagnetické vlně. Kromě toho, pokud je frekvence oscilace ve viditelném spektru, mluvíme o polarizovaném světle..
Dále uvidíme typy polarizace a fyzikální jevy, které produkují polarizované světlo..
Rejstřík článků
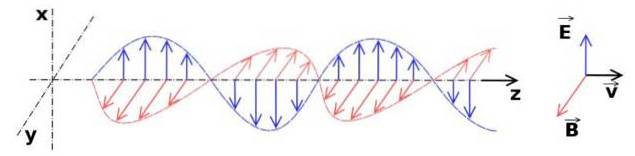
Lineární polarizace nastává, když rovina oscilace elektrického pole světelné vlny má jediný směr, kolmý ke směru šíření. Tato rovina je podle konvence brána jako rovina polarizace.
A magnetická složka se chová stejně: její směr je kolmý na elektrickou složku vlny, je jedinečný a je také kolmý na směr šíření..
Horní obrázek ukazuje lineárně polarizovanou vlnu. V zobrazeném případě vektor elektrického pole osciluje rovnoběžně s osou X, zatímco vektor magnetického pole osciluje současně s elektrickým, ale ve směru Y. Obě oscilace jsou kolmé ke směru šíření Z..
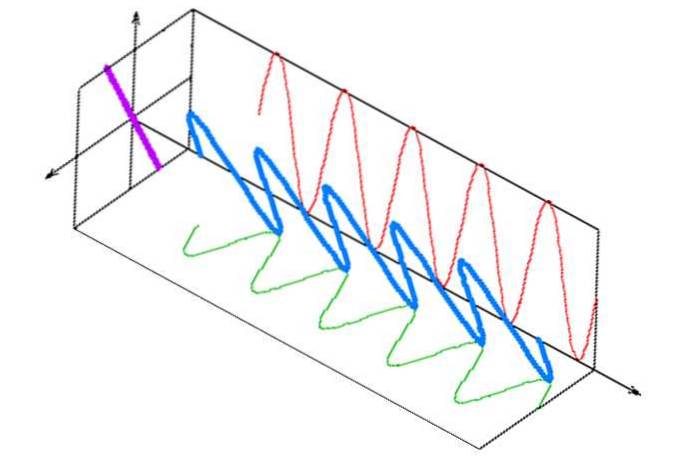
Šikmou lineární polarizaci lze dosáhnout v důsledku superpozice dvou vln, které oscilují ve fázi a mají ortogonální polarizační roviny, jak je znázorněno na obrázku níže, kde je oscilační rovina elektrického pole ve světelné vlně zobrazena modře ..
V tomto případě má amplituda elektrického a magnetického pole světelné vlny konstantní velikost, ale její směr se otáčí s konstantní úhlovou rychlostí ve směru příčném ke směru šíření..
Dolní obrázek ukazuje rotaci amplitudy elektrického pole (v červené barvě). Tato rotace je výsledkem součtu nebo superpozice dvou vln se stejnou amplitudou a lineárně polarizovaných v ortogonálních rovinách, jejichž fázový rozdíl je π / 2 radiány. Na následujícím obrázku jsou znázorněny jako modré a zelené vlny.
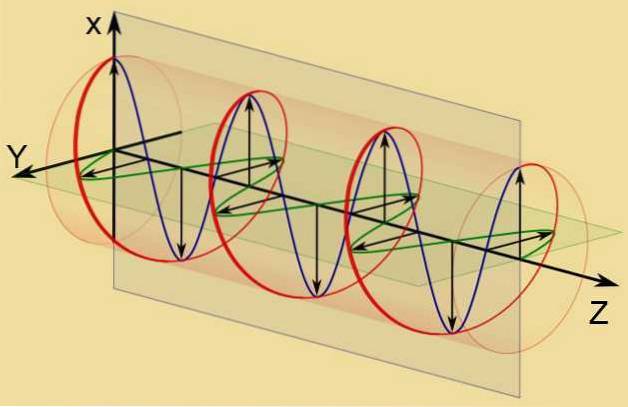
Způsob, jak psát komponenty matematicky X a Y elektrického pole vlny s pravá kruhová polarizace, amplituda Eo a to se šíří ve směru z to je:
A = (Př i; Ahoj j; Ez k) = Eo (Cos [(2π / λ) (c t - z)] i; Cos [(2π / λ) (c t - z) - π / 2] j; 0 k)
Místo toho vlna s levá ruka kruhová polarizace amplitudy Eo který se šíří ve směru z je reprezentován:
A = (Př i; Ahoj j; Ez k) = Eo (Cos [(2π / λ) (c t - z)] i, Cos [(2π / λ) (c t - z) + π / 2] j, 0 k)
Všimněte si, že znaménko se mění fázovým rozdílem čtvrtvlny komponenty Y, týkající se součásti X.
Tolik pro případ dextro-rotační Co levák, vektor magnetického pole B souvisí s vektorem elektrického pole A vektorovým součinem mezi jednotkovým vektorem ve směru šíření a A, včetně měřítka rovného inverzní rychlosti světla:
B = (1 / c) neboz ｘ A
Eliptická polarizace je podobná kruhové polarizaci, s tím rozdílem, že se amplituda pole otáčí a popisuje elipsu místo kruhu..
Vlna s eliptickou polarizací je superpozicí dvou lineárně polarizovaných vln v kolmých rovinách s předstihem nebo zpožděním π / 2 radiány ve fázi jedné vzhledem k druhé, ale s dodatkem, že amplituda pole v každé ze složek je odlišná.
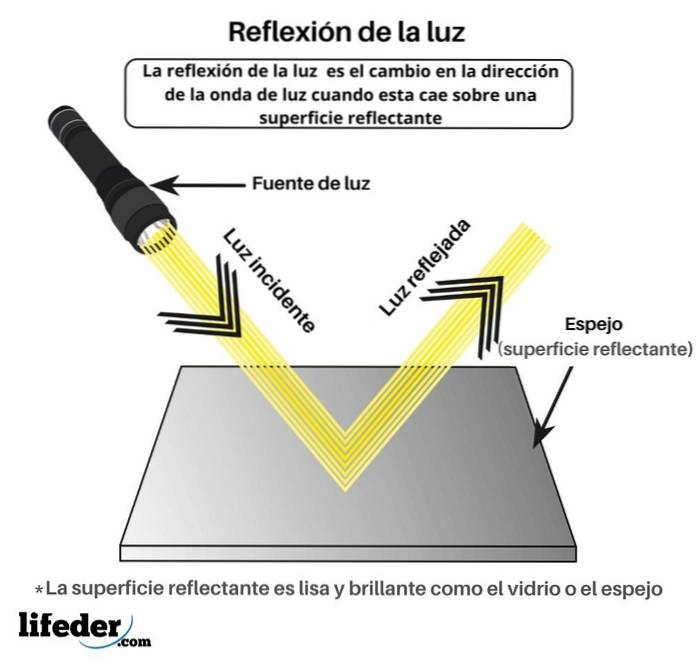
Když nepolarizovaný světelný paprsek narazí na povrch, například sklo nebo povrch vody, část světla se odráží a část se přenáší. Odražená složka je částečně polarizovaná, pokud není dopad paprsku kolmý k povrchu.
V konkrétním případě, že úhel odraženého paprsku svírá s procházejícím paprskem pravý úhel, má odražené světlo úplnou lineární polarizaci ve směru kolmém k rovině dopadu a rovnoběžně s odraznou plochou. Úhel dopadu, který produkuje celkovou polarizaci odrazem, je známý jako Brewsterův úhel.
Některé materiály umožňují selektivní přenos určité roviny polarizace elektrické složky světelné vlny.
Jedná se o vlastnost používanou pro výrobu polarizačních filtrů, ve kterých se obecně používá polymer na bázi jódu, natažený na maximum a zarovnaný jako mřížka, zhutněná mezi dvěma skleněnými tabulemi..
Takové uspořádání funguje jako vodivá mřížka, která „zkratuje“ elektrickou složku vlny podél drážek a umožňuje příčným složkám procházet polymerním svazkem. Procházející světlo je tak polarizováno v příčném směru striata.
Umístěním druhého polarizačního filtru (nazývaného analyzátor) na již polarizované světlo lze dosáhnout efektu závěrky..
Když se orientace analyzátoru shoduje s rovinou polarizace dopadajícího světla, prochází všechno světlo, ale pro ortogonální směr je světlo zcela zhasnuto.
Pro mezilehlé polohy existuje částečný průchod světla, jehož intenzita se mění podle Zákon Malus:
I = Io Cosdva(θ).
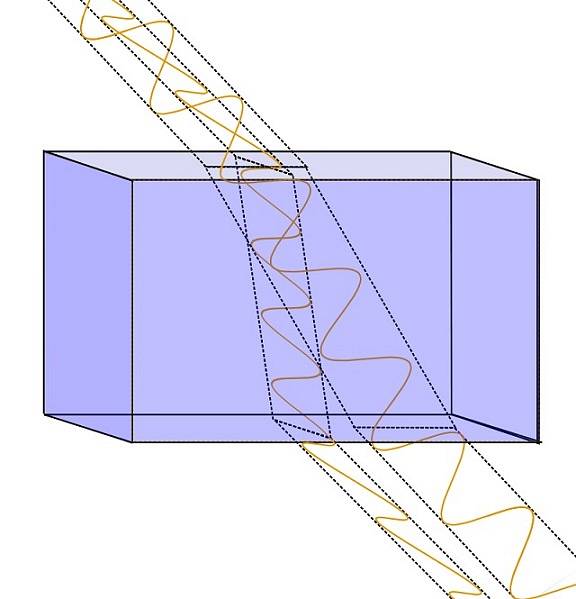
Světlo ve vakuu se jako všechny elektromagnetické vlny šíří rychlostí C přibližně 300 000 km / s. Ale v průsvitném médiu jeho rychlost proti je to o něco méně. Kvocient mezi C Y proti to se nazývá index lomu průsvitného média.
V některých krystalech, jako je kalcit, je index lomu pro každou polarizační složku odlišný. Z tohoto důvodu, když světelný paprsek prochází sklem s dvojlomem, je paprsek rozdělen na dva paprsky s lineární polarizací v ortogonálních směrech, což je ověřeno filtrem polarizátoru a analyzátoru..
Světlo odražené od hladiny mořské nebo jezerní vody je částečně polarizované. Světlo z modré oblohy, ale ne z mraků, je částečně polarizované.
Některý hmyz má rád brouka Cetonia aurata odráží světlo s kruhovou polarizací. Níže uvedený obrázek ukazuje tento zajímavý jev, při kterém lze světlo odražené broukem postupně pozorovat bez filtrů, s pravým polarizačním filtrem a poté s levým polarizačním filtrem..
Kromě toho bylo umístěno zrcadlo, které vytváří obraz s obráceným stavem polarizace ve srovnání se světlem přímo odráženým broukem..
Polarizační filtry se používají ve fotografii k eliminaci oslnění produkovaného odraženým světlem od reflexních povrchů, jako je voda..
Používají se také k eliminaci oslnění vytvářeného částečně polarizovaným světlem modré oblohy, čímž se získávají lepší kontrastní fotografie..
V chemii, stejně jako v potravinářském průmyslu, nástroj zvaný polarimetr, který umožňuje měřit koncentraci určitých látek, které v roztoku vytvářejí rotaci polarizačního úhlu.
Například průchodem polarizovaného světla a pomocí polarimetru lze rychle určit koncentraci cukru v džusech a nápojích, aby se ověřilo, že odpovídá normám výrobce a zdravotním kontrolám..
Zatím žádné komentáře