
Vlastnosti pravidelných mnohoúhelníků, prvky, úhly, příklady
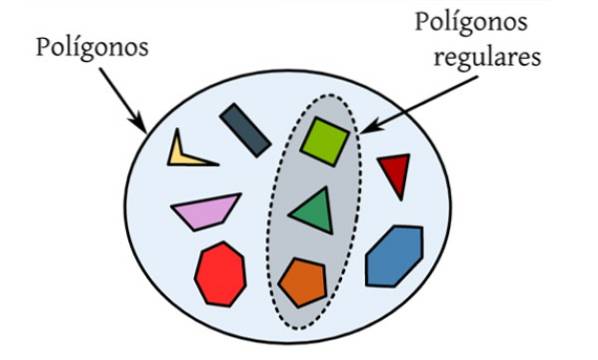
The pravidelné mnohoúhelníky jsou ti, kteří mají všechny své strany a své vnitřní úhly stejné. Na následujícím obrázku je sada různých polygonů, což jsou rovinné postavy omezené uzavřenou křivkou a pouze ty, které jsou zvýrazněny, splňují podmínky pravidelnosti.
Například rovnostranný trojúhelník je pravidelný mnohoúhelník, protože jeho tři strany měří stejně, stejně jako jeho vnitřní úhly, které mají hodnotu 60 °..
Čtverec je čtyřúhelník se čtyřmi stranami stejné míry a jehož vnitřní úhly jsou 90 °. Za ním následuje pravidelný pětiúhelník s pěti stranami stejné velikosti a pěti vnitřními úhly po 108 °..
Když je mnohoúhelník pravidelný, přidá se toto slovo k jeho speciálnímu jménu, takže máme pravidelný šestiúhelník, pravidelný sedmiúhelník atd..
Rejstřík článků
- 1 Vlastnosti pravidelných polygonů
- 2 Prvky pravidelného mnohoúhelníku
- 2.1 Vrchol
- 2.2 Boční
- 2.3 Úhlopříčka
- 2.4 Střed
- 2.5 Rádio
- 2.6 Apothem
- 2.7 Středový úhel
- 2,8 Sagita
- 3 Obvod a plocha
- 3.1 Obvod
- 3.2 Plocha
- 4 úhly
- 4.1 Středový úhel
- 4.2 Vnitřní úhel nebo vnitřní úhel
- 4.3 Vnější úhly
- 5 Příklady pravidelných polygonů
- 5.1 - Pravidelné polygony v každodenním životě a v přírodě
- 5.2 - Pravidelné šestiúhelníky v přírodě
- 6 Cvičení vyřešeno
- 6.1 Řešení
- 7 Reference
Vlastnosti pravidelných polygonů
Nejdůležitější vlastnosti pravidelných polygonů lze shrnout takto:
-Boky měří stejně, proto jsou rovnostranný.
-Oni jsou rovnoramenný, protože všechny jeho vnitřní úhly mají stejnou míru.
-Vždy je lze vepsat do obvodu, což znamená, že dokonale zapadají do jednoho, kterému se říká ohraničený obvod.
-Pro běžný mnohoúhelník s n stranami je míra vnitřního úhlu α:
a = [180 (n-2)] / n
-Z vrcholů mnohoúhelníku můžete kreslit n (n-3) / 2 úhlopříčky, ať už jsou pravidelné nebo ne.
-Součet vnější úhly se rovná 360 °.

Prvky pravidelného mnohoúhelníku
Dále představujeme hlavní prvky pravidelného mnohoúhelníku, vizualizované na obrázku níže.

Vrchol
Společný bod, který mají dvě po sobě jdoucí strany, na obrázku označený jako V..
Boční
Je to segment, který spojuje dva po sobě jdoucí vrcholy mnohoúhelníku a je označen jako ℓ nebo L.
Úhlopříčka
Segment, který spojuje dva po sobě následující vrcholy mnohoúhelníku, na obrázku je označen jako d.
Centrum
Jedná se o společný střed vepsané kružnice a opsané kružnice, označený písmenem O. Lze jej také považovat za jediný bod ve stejné vzdálenosti od obou vrcholů a středů každé strany..
Rádio
Je to rádio r popsané kružnice a shoduje se se vzdáleností mezi O a vrcholem.
Apothem
To se nazývá apothem k poloměru obvodu zapsaného do mnohoúhelníku, představovaného na obrázku písmenem na. Apothem je kolmý na jednu stranu a spojuje jej se středem O (červený segment na obrázku 3).
Známe-li poloměr r a délku strany, apotém se vypočítá podle:
Protože ve skutečnosti je apothem jednou z nohou pravoúhlého trojúhelníku (viz obrázek 3), druhou nohou je hodnota ℓ / 2 (polovina strany) a přepona poloměr r mnohoúhelníku.
Když se na uvedený trojúhelník aplikuje Pythagorova věta, získá se tato rovnice, která platí nejen pro šestiúhelník, ale pro jakýkoli regulární polygon.
Středový úhel
Je to úhel, jehož vrchol se shoduje se středem O a jehož strany jsou segmenty, které spojují střed se dvěma po sobě následujícími vrcholy. Jeho míra v sexagesimálních stupních je 360 ° / n, kde n je počet stran mnohoúhelníku.
Sagita
Je to rozdíl mezi poloměrem mnohoúhelníku a apothemem (viz obrázek 3). Označujeme sagittu jako S:
S = r - a
Obvod a plocha
Obvod
Snadno se vypočítá přidáním délek stran. Jelikož kterákoli strana má stejnou délku L a existuje n stran, je obvod P vyjádřen jako:
P = n.L
Plocha
V pravidelném polygonu je plocha A dána součinem mezi poloobvodem (polovina obvodu) a délkou apotému na.
A = P.a / 2
Protože obvod závisí na počtu stran n, ukazuje se, že:
A = (nL) .a / 2
Dva pravidelné polygony mohou mít stejný obvod, i když nemají stejný počet stran, protože by to pak záleželo na délce stran.
V knize V jeho Sbírka, matematik Pappus Alexandrijský (290–350), poslední z velkých starořeckých matematiků, ukázal, že ze všech pravidelných mnohoúhelníků se stejným obvodem je ten s největší plochou ten, který má největší počet stran.
Úhly
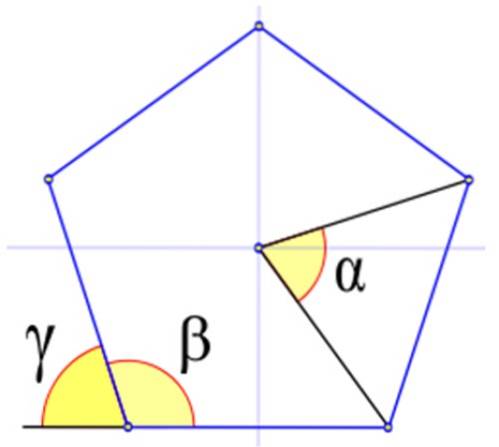
Obrázek 4 ukazuje příslušné úhly v pravidelném mnohoúhelníku, které jsou označeny řeckými písmeny α, β a γ.
Středový úhel
Dříve jsme zmínili středový úhel, mezi prvky pravidelného mnohoúhelníku je to úhel, jehož vrchol je ve středu mnohoúhelníku a po stranách jsou segmenty, které spojují střed se dvěma po sobě následujícími vrcholy.
Chcete-li vypočítat míru středového úhlu α, vydělte 360 ° číslem n, počtem stran. Nebo 2π radiány mezi n:
α = 360 ° / n
Ekvivalent v radiánech na:
α = 2π / n
Vnitřní úhel nebo vnitřní úhel
Na obrázku 4 je vnitřní úhel β úhel, jehož vrchol se shoduje s jedním z obrazce a jeho strany jsou také stranami obrazce. Vypočítává se v sexageimálních stupních podle:
β = [180 (n-2)] / n
Nebo v radiánech pomocí:
β = [π (n-2)] / n
Vnější úhly
Jsou označeny řeckým písmenem γ. Obrázek ukazuje, že γ + β = 180 °. Proto:
γ = 180º - β
Součet všech vnějších úhlů k pravidelnému mnohoúhelníku je 360 °.

Příklady pravidelných polygonů
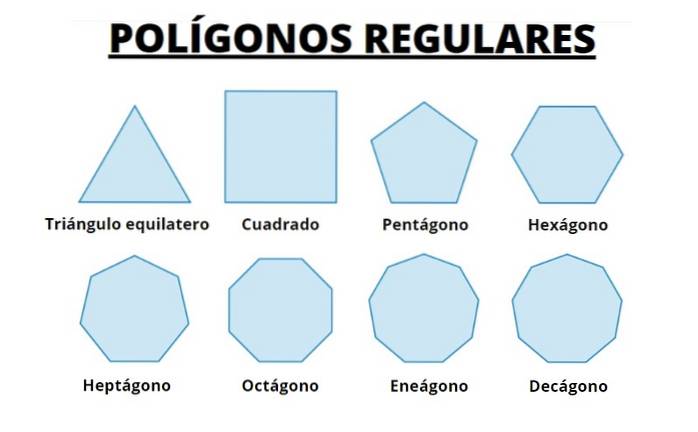
Dále máme prvních 8 pravidelných polygonů. Pozorujeme, že s rostoucím počtem stran se polygon stále více podobá obvodu, ve kterém jsou vepsány.
Dokážeme si představit, že zmenšením a zmenšením délky stran získáme obvod.
- Pravidelné mnohoúhelníky v každodenním životě a v přírodě
Pravidelné mnohoúhelníky se nacházejí všude v každodenním životě a dokonce i v přírodě. Podívejme se na několik příkladů:
Dopravní signály
Značení, které vidíme na dálnicích a silnicích, je plné pravidelných polygonů, jako jsou rovnostranné trojúhelníky, čtverce a kosočtverce. Na obrázku 6 vidíme stopku s osmibokým tvarem.

Nábytek
Nespočet kusů nábytku má například čtverec jako svou charakteristickou geometrickou postavu, stejně jako mnoho stolů, židlí a lavic je čtvercových. Rovnoběžník je obvykle krabice se stranami ve tvaru obdélníku (který není pravidelným mnohoúhelníkem), ale lze je také vytvořit čtvercovou..
Architektura a stavebnictví
Dlaždice na podlahách a stěnách, v domácnostech i na ulicích, mají často tvar pravidelných mnohoúhelníků..
Teselace jsou povrchy zcela pokryté dlaždicemi, které mají různé geometrické tvary. S trojúhelníkem, čtvercem a šestiúhelníkem můžete vytvářet pravidelné mozaikování, ty, které k dokonalému zakrytí používají pouze jeden typ obrázku, aniž by zbyly prázdné mezery (viz obrázek 6).
Podobně budovy využívají pravidelné mnohoúhelníky v prvcích, jako jsou okna a dekorace..

- Pravidelné šestiúhelníky v přírodě
Pravidelným šestiúhelníkem je překvapivě mnohoúhelník, který se v přírodě často objevuje..
Hřebeny vyrobené včelami k ukládání medu jsou tvarovány velmi blízko pravidelného šestiúhelníku. Jak poznamenal Pappus z Alexandrie, včely tímto způsobem optimalizují prostor pro ukládání co největšího množství medu..
A ve skořápce želv a sněhových vloček jsou také pravidelné šestiúhelníky, které také přijímají různé velmi krásné geometrické tvary..
Cvičení vyřešeno
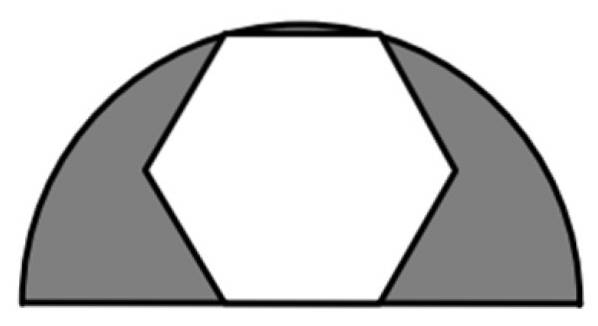
Pravidelný šestiúhelník je vepsán do půlkruhu o poloměru 6 cm, jak je znázorněno na obrázku. Jaká je hodnota stínované oblasti?
Řešení
Stínovaná plocha je rozdíl mezi plochou půlkruhu s poloměrem R = 6 cm a plochou celého šestiúhelníku, což je pravidelný šestiboký polygon. Budeme tedy potřebovat vzorce pro plochu každého z těchto čísel.
Oblast půlkruhu
NA1 = π Rdva / 2 = π (6 cm)dva / 2 = 18π cmdva
Pravidelná šestihranná plocha
Vzorec pro výpočet plochy pravidelného mnohoúhelníku je:
A = P.a / 2
Kde P je obvod a na je apothem. Protože obvod je součtem stran, budeme potřebovat jejich hodnotu. Pro běžný šestiúhelník:
P = 6ℓ
Proto:
A = 6ℓa / 2
Pro zjištění hodnoty strany ℓ je nutné sestrojit pomocné obrázky, které vysvětlíme níže:
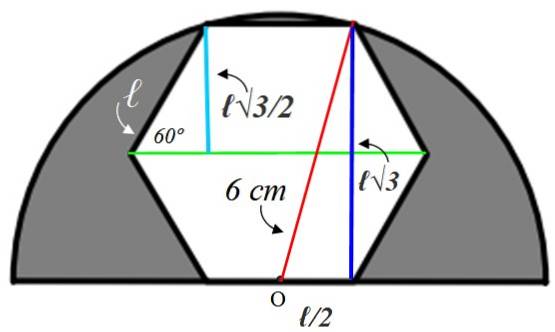
Začněme malým pravým trojúhelníkem vlevo, jehož přepona je ℓ. Vnitřní úhel šestiúhelníku se rovná:
a = [180 (n-2)] / n = a = [180 (6-2)] / 6 = 120 °
Poloměr, který jsme nakreslili zeleně, půlí tento úhel, proto je ostrý úhel malého trojúhelníku 60 °. S poskytnutými informacemi je tento trojúhelník vyřešen a najde světle modrou stranu, která měří stejně jako apothem:
Opak nohy = a = ℓ x sin 60º = ℓ√3 / 2 cm
Tato hodnota je to dvojnásobek tmavě modré nohy velkého trojúhelníku vpravo, ale z tohoto trojúhelníku víme, že přepona měří 6 cm, protože je to poloměr půlkruhu. Zbývající noha (dole) se rovná ℓ / 2, protože bod O je uprostřed strany.
Jelikož vnitřní úhly tohoto trojúhelníku nejsou známy, můžeme pro něj uvést Pythagorovu větu:
36 = 3 ℓdva + ℓdva / 4
(13/4) ℓdva = 36 → ℓ = √ (4 x36) / 13 cm = 12 / √13 cm
S touto hodnotou se počítá apothem:
a = ℓ√3 / 2 cm = (12 / √13) x (√3 / 2) cm = 6√3 / √13 cm
Zavolejmedva do oblasti pravidelného šestiúhelníku:

= 28,8 cmdva
Stínovaná plocha obrázku
NA1 - NAdva = 18π cmdva - 28,8 cmdva = 27,7 cmdva
Reference
- Baldor, A. 1973. Geometrie a trigonometrie. Středoamerické kulturní nakladatelství.
- Užijte si matematiku. Mozaikování. Obnoveno z: gustolasmatematicas.com.
- E. A. 2003. Prvky geometrie: cvičení a geometrie kompasu. University of Medellin.
- Šestiúhelníky v přírodě. Obnoveno z: malvargamath.wordpress.com.
- Jiménez, R. 2010. Matematika II. Geometrie a trigonometrie. Druhé vydání. Hala Prentice.
- Pravidelné mnohoúhelníky. Obnoveno z: mate.ingenieria.usac.edu.gt.
- Wikipedia. Apothem. Obnoveno z: es.wikipedia.org.

Zatím žádné komentáře