The měřicí tlak Pm je to, co se měří ve vztahu k referenčnímu tlaku, který se ve většině případů volí jako atmosférický tlak Pbankomat na úrovni moře. To je pak a relativní tlak, jiný termín, pod kterým je také známý.
Druhým způsobem, jakým se obvykle měří tlak, je jeho porovnání s absolutním vakuem, jehož tlak je vždy nulový. V takovém případě mluvíme o absolutní tlak, kterou označíme jako Pna.
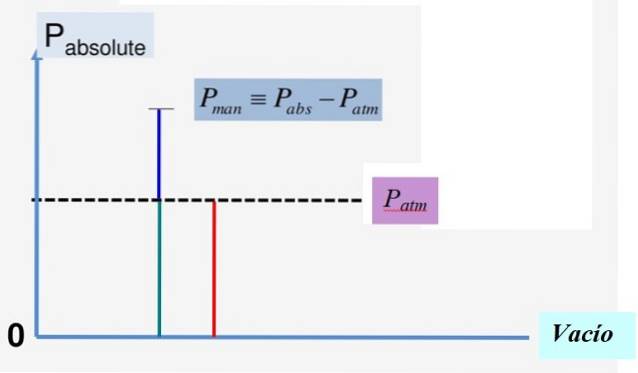
Matematický vztah mezi těmito třemi veličinami je:
Pna = Pbankomat + Pm
Proto:
Pm = Pna - Pbankomat
Obrázek 1 pohodlně ilustruje tento vztah. Protože vakuový tlak je 0, je absolutní tlak vždy kladný a to samé se děje s atmosférickým tlakem Pbankomat.
Měřicí tlak se často používá k označení tlaků nad atmosférickým tlakem, jako je tlak nacházející se v pneumatikách nebo na dně moře nebo v bazénu, který je vyvíjen váhou vodního sloupce. V těchto případech Pm > 0, protože Pna > Pbankomat.
Existují však absolutní tlaky pod Pbankomat. V těchto případech Pm < 0 y recibe el nombre de Tlak z prázdný a nezaměňovat s tlakem z vakuum již popsané, což je nepřítomnost částic schopných vyvinout tlak.
Rejstřík článků
Tlak v kapalině - kapalině nebo plynu - je jednou z nejvýznamnějších proměnných v její studii. Ve stacionární tekutině je tlak ve všech bodech ve stejné hloubce stejný bez ohledu na orientaci, zatímco pohyb tekutin v potrubí je způsoben změnami tlaku..
Střední tlak je definován jako podíl mezi silou kolmou k povrchu F⊥ a plocha uvedeného povrchu A, která je matematicky vyjádřena takto:
P = F⊥ /NA
Tlak je skalární veličina, jejíž rozměry jsou síla na jednotku plochy. Jednotky jeho měření v mezinárodním systému jednotek (SI) jsou newton / mdva, volal Pascal a ve zkratce Pa, na počest Blaise Pascala (1623-1662).
Násobky jako kilo (103) Y mega (106) se často používají, protože atmosférický tlak je obvykle v rozmezí 90 000 - 102 000 Pa, což se rovná: 90 - 102 kPa. Tlak v řádu megapascalů není neobvyklý, proto je důležité seznámit se s předponami.
V anglosaských jednotkách se tlak měří v librách / stopudva, obvykle se to však děje v librách / palecdva nebo psi (liber síla na čtvereční palec).
Čím více se ponoříme do vody v bazénu nebo v moři, tím větší tlak zažijeme. Se zvyšující se výškou se naopak snižuje atmosférický tlak.
Průměrný atmosférický tlak na hladině moře je stanoven na 101 300 Pa nebo 101,3 kPa, zatímco v Mariánské příkopě v západním Pacifiku - nejhlubší známé hloubce - je asi 1000krát větší a na vrcholu Everestu je to jen 34 kPa.
Je zřejmé, že tlak a hloubka (nebo výška) spolu souvisejí. Chcete-li zjistit v případě kapaliny v klidu (statická rovnováha), uvažuje se část kapaliny ve tvaru disku uzavřená v nádobě (viz obrázek 2). Disk má plochu průřezu NA, hmotnost dW a výška dy.
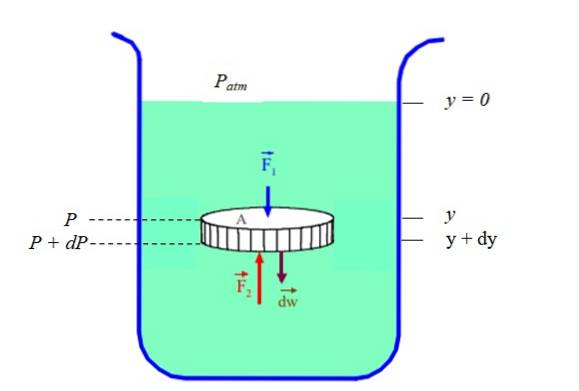
Zavoláme P tlaku, který existuje v hloubce “Y„Y P + dP tlaku, který existuje v hloubce (y + dy). Protože hustota ρ kapaliny je poměrem její hmotnosti dm a jeho objem dV, musíš:
ρ = dm / dV ⇒ dm = ρ.dV
Proto váha dW prvku je:
dW = g. dm = ρ.g.dV
A nyní platí druhý Newtonův zákon:
Σ FY = Fdva - F1 - dW = 0
(P + dP). A - P.A - ρ.g.dV = 0
(P + dP). A - P.A - ρ.G. A. dy = 0
dP = ρ.g.dy
Integrace obou stran a vzhledem k tomu, že hustota ρ, stejně jako gravitace G jsou konstantní, hledaný výraz je nalezen:
Pdva - P1 = ΔP = ρ.g. (adva - Y1)
ΔP = ρ.G. ΔY
Pokud v předchozím výrazu zvolíte P1 jako atmosférický tlak a Y1 jako povrch kapaliny Ydva nachází se v hloubce h Y ΔP = Pdva - Pbankomat je přetlak jako funkce hloubky:
Pm = ρ.h. h
V případě, že potřebujete hodnotu absolutního tlaku, jednoduše přidejte atmosférický tlak k předchozímu výsledku.
Pro měření tlaku měřidla volalo zařízení tlakoměr, které obecně nabízejí tlakové rozdíly. Na konci bude popsán pracovní princip U-trubkového manometru, ale nyní se podívejme na několik důležitých příkladů a důsledků dříve odvozené rovnice.
Rovnice ΔP = ρ.g. (adva - Y1) lze psát jako P = Po + ρ.h. h, kde P je tlak v hloubce h, zatímco Pnebo je tlak na povrchu tekutiny, obvykle Pbankomat.
Je zřejmé, že pokaždé, když se zvýší Po, zvyšuje P ve stejném množství, pokud je to tekutina, jejíž hustota je konstantní. Je to přesně to, co se předpokládalo při zvažování ρ konstanta a umístit ji mimo integrál vyřešený v předchozí části.
Pascalův princip uvádí, že jakékoli zvýšení tlaku uzavřené tekutiny v rovnováze se přenáší bez jakékoli změny do všech bodů uvedené tekutiny. Prostřednictvím této vlastnosti je možné znásobit sílu F1 aplikujte na malý píst vlevo a získejte Fdva napravo.
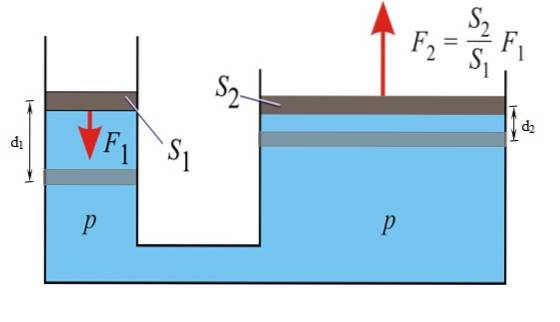
Brzdy automobilů fungují na tomto principu: na pedál působí relativně malá síla, která se díky kapalině použité v systému stává větší silou na brzdový válec na každém kole..
Hydrostatický paradox uvádí, že síla způsobená tlakem kapaliny na dně nádoby může být stejná, větší nebo menší než hmotnost samotné kapaliny. Když ale dáte nádobu na váhu, bude to normálně registrovat hmotnost kapaliny (samozřejmě plus váhu nádoby). Jak vysvětlit tento paradox?
Vycházíme ze skutečnosti, že tlak na dně nádoby závisí výhradně na hloubce a je nezávislý na tvaru, jak bylo odvozeno v předchozí části.
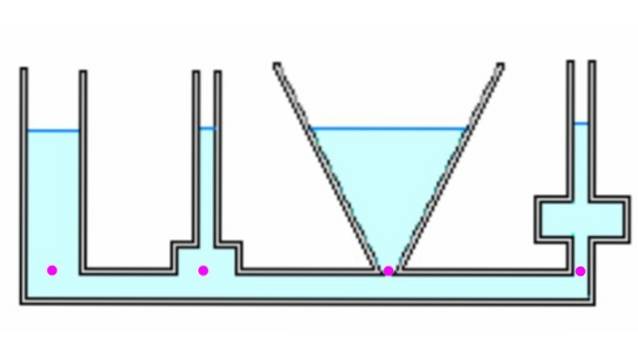
Podívejme se na několik různých kontejnerů. Když se sdělí, když se naplní kapalinou, všichni dosáhnou stejné výšky h. Zvýraznění je pod stejným tlakem, protože je ve stejné hloubce. Síla způsobená tlakem v každém bodě se však může lišit od hmotnosti (viz příklad 1 níže).
Porovnejte sílu vyvíjenou tlakem na dno každé z nádob s hmotností tekutiny a vysvětlete, proč jsou rozdíly, pokud existují.
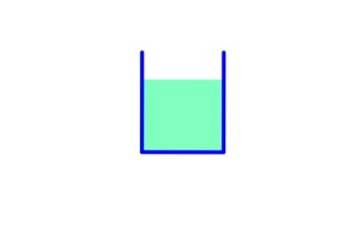
V tomto kontejneru je plocha základny A, proto:
Hmotnost kapaliny: mg = ρ.V.g = ρ . A .h. G
Tlak na dno: ρ. G. h
Síla v důsledku tlaku: F = P.A = ρ. G. h. NA
Hmotnost a síla způsobená tlakem jsou stejné.
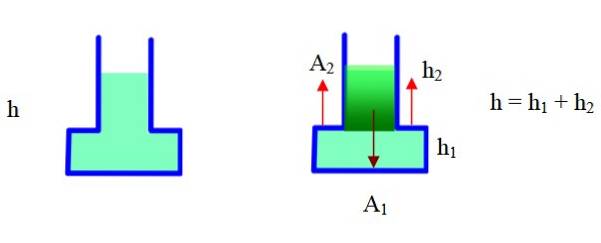
Kontejner má úzkou část a širokou část. V diagramu vpravo byl rozdělen na dvě části a geometrie bude použita k nalezení celkového objemu. Oblast Adva to je externí do kontejneru, hdva je výška úzké části, h1 je výška široké části (základny).
Celý objem je objem základny + objem úzké části. S těmito údaji máme:
Hmotnost kapaliny: m. g = ρ . G. V = ρ . G. [NA1 .h1+ (NA1 -NAdva) .hdva] =
= ρ . g (A.1.hadvahdva) = ρ . G. NA1.h - ρ . G. NA.. hdva (Bylo použito h = h1 +hdva)
Tlak na dně: P = ρ. G. h
Síla na dno v důsledku tlaku: F = P. A1 = ρ. G. h. NA1
Porovnání hmotnosti kapaliny se silou způsobenou tlakem ukazuje, že je to větší než hmotnost.
Co se stane, je, že kapalina také vyvíjí sílu na část kroku v nádobě (viz červené šipky na obrázku), které jsou zahrnuty ve výše uvedeném výpočtu. Tato síla vzhůru působí proti těm, kteří působí směrem dolů, a váha zaznamenaná stupnicí je jejich výsledkem. Podle toho je velikost váhy:
W = Síla na dně - Síla na stupňovitou část = ρ . G. NA1.h - ρ . G. NA.. hdva
Otevřený tubusový manometr je znázorněn na obrázku. Skládá se z trubice ve tvaru U, ve které je jeden konec za atmosférického tlaku a druhý je připojen k S, systému, jehož tlak se má měřit..
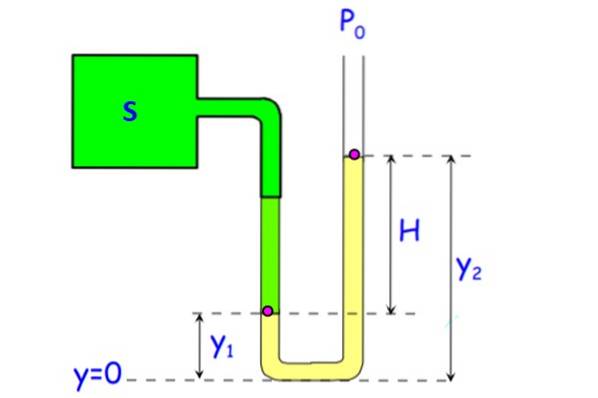
Kapalinou v trubici (na obrázku znázorněnou žlutě) může být voda, i když ke zmenšení velikosti zařízení se přednostně používá rtuť. (Rozdíl 1 atmosféry nebo 101,3 kPa vyžaduje 10,3 metrů vodní sloupec, nic přenosného).
Požádá o nalezení tlaku měřidla Pm v systému S, jako funkce výšky H sloupce kapaliny.
Tlak na dně obou větví trubky je stejný, protože jsou ve stejné hloubce. Ať PNA tlak v bodě A, který se nachází v y1 A strB ty z bodu B, které jsou ve výšce adva. Protože bod B je na rozhraní kapaliny a vzduchu, je zde tlak Pnebo. V této větvi manometru je tlak ve spodní části:
Po + ρ.g.ydva
Tlak dole pro větev vlevo je:
P + ρ.g.y.1
Kde P je absolutní tlak systému a ρ je hustota kapaliny. Vyrovnání obou tlaků:
Po + ρ.g.ydva = P + ρ.g.y.1
Čistí se P:
P = Po + ρ.g.y.dva - ρ.g.y.1 = Po + ρ.g (adva - Y1) = Po + ρ.g. H
Proto je měřicí tlak Pm darováno P - Pnebo = ρ.g. H a abyste získali jeho hodnotu, změřte pouze výšku, do které manometrická kapalina stoupá, a vynásobte ji hodnotou G a hustota kapaliny.
Zatím žádné komentáře