Čtyřhranný hranolový vzorec a objem, charakteristiky

A Čtvercový hranol Je to ten, jehož povrch je tvořen dvěma stejnými základnami, které jsou čtyřúhelníky, a čtyřmi bočními plochami, které jsou rovnoběžníky. Mohou být klasifikovány podle úhlu sklonu a tvaru základny.

Hranol je nepravidelné geometrické těleso, které má ploché plochy a tyto uzavírají konečný objem, který je založen na dvou polygonech a bočních plochách, které jsou rovnoběžníky. Podle počtu stran mnohoúhelníků základen mohou být hranoly mimo jiné: trojúhelníkové, čtyřúhelníkové, pětiúhelníkové.

Charakteristiky, kolik má ploch, vrcholů a hran?

Hranol se čtyřhrannou základnou je polyedrický útvar, který má dvě stejné a rovnoběžné základny a čtyři obdélníky, které jsou bočními plochami, které spojují odpovídající strany obou základen..

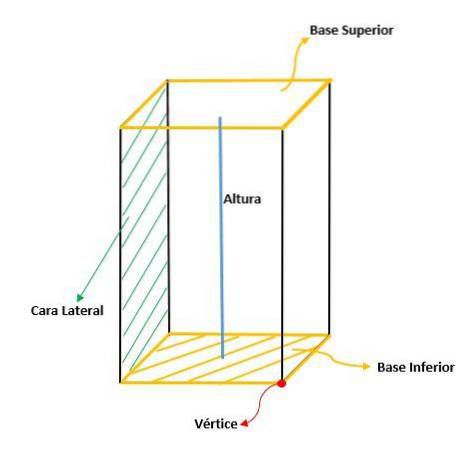
Čtyřhranný hranol lze odlišit od ostatních typů hranolů, protože má následující prvky:

Základny (B)

Jsou to dva polygony tvořené čtyřmi stranami (čtyřúhelník), které jsou stejné a rovnoběžné.

Tváře (C)

Celkově má ​​tento typ hranolu šest tváří:

• Čtyři boční plochy tvořené obdélníky.
• Dvě tváře, které jsou čtyřúhelníky, které tvoří základny.

Vrcholy (V)

Jsou to ty body, kde se shodují tři tváře hranolu, v tomto případě je celkem 8 vrcholů.

Hrany: (A)

Jsou to segmenty, kde se setkávají dvě tváře hranolu, a to jsou:

• Okraje základny: jedná se o spojovací čáru mezi boční plochou a základnou, celkem jich je 8.
• Boční hrany: je to boční spojovací čára mezi dvěma plochami, celkem jsou 4.

Počet hran mnohostěnu lze také vypočítat pomocí Eulerovy věty, pokud je znám počet vrcholů a ploch; pro čtyřúhelníkový hranol se tedy počítá takto:

Počet hran = počet ploch + počet vrcholů - 2.

Počet hran = 6 + 8 - 2.

Počet hran = 12.

Výška (h)

Výška čtyřúhelníkového hranolu se měří jako vzdálenost mezi jeho dvěma základnami.

Klasifikace

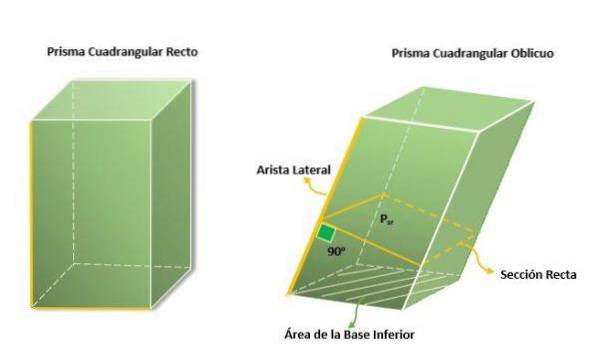
Čtyřhranné hranoly lze klasifikovat podle úhlu sklonu, který může být rovný nebo šikmý:

Pravoúhlé hranoly

Mají dvě stejné a rovnoběžné plochy, které jsou základnami hranolu, jejich boční plochy jsou tvořeny čtverci nebo obdélníky, tímto způsobem jsou všechny jejich boční hrany stejné a jejich délka se bude rovnat výšce hranolu.

Celková plocha je určena plochou a obvodem její základny, výškou hranolu:

V = A_boční + 2A_základna.

Šikmé čtyřhranné hranoly

Tento typ hranolu se vyznačuje tím, že jeho boční plochy tvoří šikmé vzepětí s bázemi, to znamená, že její boční plochy nejsou kolmé k základně, protože mají stupeň sklonu, který může být menší než nebo větší než 90^nebo.

Jeho boční plochy jsou obecně rovnoběžníky s kosočtverečným nebo kosodélníkovým tvarem a mohou mít jednu nebo více obdélníkových ploch. Další charakteristikou těchto hranolů je, že jejich výška se liší od měření jejich bočních hran..

Plocha šikmého čtyřúhelníkového hranolu se vypočítá téměř stejně jako předchozí, přičemž se přidá plocha základen s boční oblastí; jediným rozdílem je způsob výpočtu jeho boční plochy.

Plocha bočnic se vypočítá s boční hranou a obvodem přímé části hranolu, což je právě místo, kde je vytvořen úhel 90^nebo s každou ze stran.

NA_celkový = 2 _* Plocha_základna + Obvod_{Pan *} Okraj_boční

Objem všech typů hranolů se vypočítá vynásobením plochy základny výškou:

V = plocha_{základna *} výška = A_{b *} h.

Stejným způsobem lze čtyřúhelníkové hranoly klasifikovat podle typu čtyřúhelníku, který tvoří báze (pravidelné a nepravidelné):

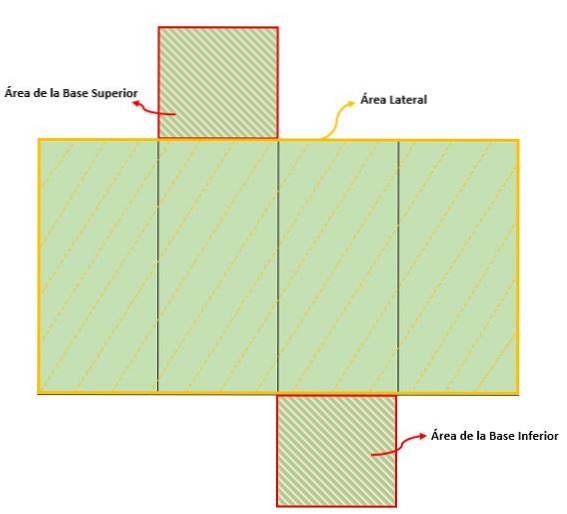
Pravidelný čtyřhranný hranol

Je to jeden, který má jako základnu dva čtverce a jeho boční plochy jsou stejné obdélníky. Jeho osa je ideální linie, která probíhá rovnoběžně s jejími tvářemi a končí ve středu jejích dvou základen..

Chcete-li určit celkovou plochu čtyřúhelníkového hranolu, musí se vypočítat plocha jeho základny a boční plochy tak, aby:

V = A_boční + 2A_základna.

Kde:

Boční plocha odpovídá ploše obdélníku; a to:

NA _boční = Základna _* Výška = B _* h.

Plocha základny odpovídá ploše čtverce:

NA _základna = 2 (boční _* Side) = 2L^dva

Chcete-li určit hlasitost, vynásobte plochu základny výškou:

V = A _{základna *} Výška = L^dva_* h

Nepravidelný čtyřhranný hranol

Tento typ hranolu se vyznačuje tím, že jeho základny nejsou čtvercové; může mít základny skládající se z nerovných stran a je prezentováno pět případů, kdy:

na. Základny jsou obdélníkové

Jeho povrch je tvořen dvěma obdélníkovými základnami a čtyřmi bočními plochami, které jsou také obdélníky, všechny stejné a rovnoběžné..

K určení jeho celkové plochy se vypočítá každá oblast šesti obdélníků, které ji tvoří, dvě základny, dvě malé boční plochy a dvě velké boční plochy:

Plocha = 2 (a_* b + a_*h + b_*h)

b. Základem jsou diamanty:

Jeho povrch je tvořen dvěma základnami ve tvaru kosočtverce a čtyřmi obdélníky, které jsou bočními plochami, pro výpočet jeho celkové plochy je třeba určit:

• Základní plocha (kosočtverec) = (hlavní úhlopříčka _* vedlejší úhlopříčka) ÷ 2.
• Lateral Area = obvod základny _* výška = 4 (strany základny) * h

Celková plocha tedy je: A_T = A_boční + 2A_základna.

C. Základny jsou kosodélníkové

Jeho povrch je tvořen dvěma základnami ve tvaru kosočtverce a čtyřmi obdélníky, které jsou bočními plochami, je jeho celková plocha dána vztahem:

• Základní plocha (kosodélník) = základna _* relativní výška = B * h.
• Lateral Area = obvod základny _* výška = 2 (strana a + strana b) _* h
• Celková plocha je tedy: A_T = A_boční + 2A_základna.

d. Základny jsou lichoběžníky

Jeho povrch je tvořen dvěma základnami ve tvaru lichoběžníků a čtyřmi obdélníky, které jsou bočními plochami, je jeho celková plocha dána vztahem:

• Základní plocha (lichoběžník) = h _* [(strana a + strana b) ÷ (2)].
• Lateral Area = obvod základny _* výška = (a + b + c + d) * h
• Celková plocha je tedy: A_T = A_boční + 2A_základna.

a. Základny jsou lichoběžníky

Jeho povrch je tvořen dvěma základnami ve tvaru lichoběžníku a čtyřmi obdélníky, které jsou bočními plochami, je jeho celková plocha dána vztahem:

• Základní plocha (lichoběžník) = = (úhlopříčka_{1 *} úhlopříčka_dva) ÷ 2.
• Lateral Area = obvod základny _* výška = 2 (strana a _* strana b * h.
• Celková plocha je tedy: A_T = A_boční + 2A_základna.

Stručně řečeno, k určení plochy jakéhokoli pravidelného čtyřúhelníkového hranolu je nutné vypočítat pouze plochu čtyřúhelníku, což je základna, jeho obvod a výška, kterou hranol bude mít, obecně by jeho vzorec byl být:

Plocha _Celkový = 2_* Plocha_základna + Obvod_{základna *} výška = A = 2A_b + P_{b *} h.

Pro výpočet objemu pro tyto typy hranolů se používá stejný vzorec, který je:

Objem = Plocha_{základna *} výška = A_{b *} h.

Reference

1. Ángel Ruiz, H. B. (2006). Geometrie. CR technologie, .
2. Daniel C. Alexander, G. M. (2014). Základní geometrie pro studenty vysokých škol. Cengage Learning.
3. Maguiña, R. M. (2011). Geometrie pozadí. Lima: UNMSM Pre-University Center.
4. Ortiz Francisco, O. F. (2017). Matematika 2.
5. Pérez, A. Á. (1998). Álvarezova encyklopedie druhého stupně.
6. Pugh, A. (1976). Mnohostěn: Vizuální přístup. Kalifornie: Berkeley.
7. Rodríguez, F. J. (2012). Popisná geometrie, svazek I. Dihedrální systém. Donostiarra Sa.