
Koncept frekvenční pravděpodobnosti, způsob jeho výpočtu a příklady
The pravděpodobnost frekvence je sub-definice v rámci studia pravděpodobnosti a jejích jevů. Jeho studijní metoda s ohledem na události a atributy je založena na velkém množství iterací, čímž sleduje trend každého z nich dlouhodobě nebo dokonce v nekonečných opakováních..
Například obálka gummies obsahuje 5 gum s každou barvou: modrou, červenou, zelenou a žlutou. Chceme určit pravděpodobnost, že každá barva musí vyjít po náhodném výběru.

Je zdlouhavé představovat si vyndání gumy, registraci, vrácení, vytažení gumy a opakování stejné věci několik set nebo několik tisíckrát. Možná budete chtít pozorovat chování po několika milionech iterací.
Naopak je zajímavé zjistit, že po několika opakováních není plně splněna očekávaná pravděpodobnost 25%, alespoň ne u všech barev po 100 iteracích..
Podle přístupu pravděpodobnosti frekvence bude přiřazení hodnot probíhat pouze studiem mnoha iterací. Tímto způsobem musí být proces prováděn a registrován nejlépe počítačově nebo emulovaným způsobem.
Několik proudů odmítá pravděpodobnost frekvence a argumentuje nedostatkem empirismu a spolehlivosti v kritériích náhodnosti.
Rejstřík článků
- 1 Jak se počítá pravděpodobnost frekvence?
- 1.1 Zákon velkých čísel
- 2 Další přístupy k pravděpodobnosti
- 2.1 Logická teorie
- 2.2 Subjektivní teorie
- 3 Historie
- 3.1 Hromadné jevy a opakující se události
- 3.2 Atributy
- 4 Příklad
- 4.1 Odkazy
Jak se počítá pravděpodobnost frekvence?
Programováním experimentu v jakémkoli rozhraní schopném nabídnout čistě náhodnou iteraci lze začít studovat frekvenční pravděpodobnost jevu pomocí tabulky hodnot.
Předchozí příklad je patrný z frekvenčního přístupu:
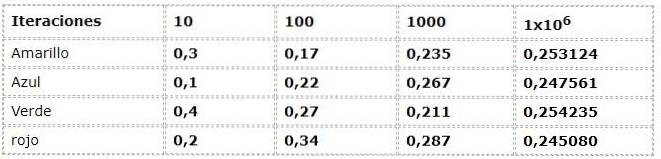
Číselné údaje odpovídají výrazu:
N (a) = počet výskytů / počet iterací
Kde N (a) představuje relativní frekvenci události „a“
„A“ patří do množiny možných výsledků nebo vzorkovacího prostoru Ω
Ω: červená, zelená, modrá, žlutá
Značná disperze je oceňována v prvních iteracích, při pozorování frekvencí s rozdíly až 30% mezi nimi, což je velmi vysoký údaj pro experiment, který má teoreticky události se stejnou možností (Rovnoměrný).
Ale jak iterace rostou, zdá se, že se hodnoty stále více přizpůsobují těm, které představují teoretický a logický proud.
Zákon velkých čísel
Jako neočekávaná shoda mezi teoretickým a frekvenčním přístupem vyvstává zákon velkého počtu. Pokud se zjistí, že po značném počtu iterací se hodnoty frekvenčního experimentu blíží teoretickým hodnotám.
V příkladu můžete vidět, jak se hodnoty s přibývajícími iteracemi blíží 0,250. Tento jev je základní v závěrech mnoha pravděpodobnostních prací.

Další přístupy k pravděpodobnosti
Kromě pojmu pravděpodobnosti existují ještě 2 další teorie nebo přístupy pravděpodobnost frekvence.
Logická teorie
Jeho přístup je zaměřen na deduktivní logiku jevů. V předchozím příkladu je pravděpodobnost získání každé barvy uzavřeným způsobem 25%. To znamená, že jejich definice a axiomy neuvažují o zpožděních mimo jejich rozsah pravděpodobnostních dat..
Subjektivní teorie
Je založen na znalostech a předchozích přesvědčeních, které má každý jedinec o fenoménech a atributech. Výroky jako „Na Velikonoce vždy prší “ Jsou způsobeny vzorem podobných událostí, ke kterým došlo dříve.
Příběh
Počátky jeho implementace sahají do 19. století, kdy jej Venn uvedl v několika svých dílech v Cambridge v Anglii. Ale až do dvacátého století vyvinuli a formovali 2 statističtí matematici pravděpodobnost frekvence.
Jedním z nich byl Hans Reichenbach, který rozvíjí svou práci v publikacích jako „The Theory of Probability“ vydaných v roce 1949.
Druhým byl Richard Von Mises, který svou práci dále rozvinul prostřednictvím několika publikací a navrhl uvažovat o pravděpodobnosti jako o matematické vědě. Tento koncept byl pro matematiku nový a ohlašoval by éru růstu studia matematiky. pravděpodobnost frekvence.
Tato událost ve skutečnosti představuje jediný rozdíl v příspěvcích generací Venna, Cournota a Helma. Kde se pravděpodobnost stává homologní k vědám, jako je geometrie a mechanika.
< La teoría de las probabilidades trata con masivní jevy a opakující se události. Problémy, při nichž se stále opakuje stejná událost, nebo je současně zapojeno velké množství jednotných prvků> Richard Von Mises
Masivní jevy a opakující se události
Lze klasifikovat tři typy:
- Fyzické: podřizují se vzorům přírody mimo podmínku náhodnosti. Například chování molekul prvku ve vzorku.
- Šance - Vaším primárním hlediskem je náhodnost, například opakované házení kostkou.
- Biologická statistika: výběr testovaných osob podle jejich charakteristik a atributů.
Teoreticky hraje roli v pravděpodobnostních datech jednotlivec, který měří, protože tuto hodnotu nebo predikci vyjadřují právě jeho znalosti a zkušenosti..
V pravděpodobnost frekvence události budou považovány za kolekce, které mají být zpracovány, kde jedinec nehraje při odhadu žádnou roli.
Atributy
Atribut se vyskytuje v každém prvku, který bude proměnlivý podle jeho povahy. Například u typu fyzikálního jevu budou mít molekuly vody různé rychlosti..
V hodu kostkami známe prostor vzorku Ω, který představuje atributy experimentu.
Ω: 1, 2, 3, 4, 5, 6
Existují i další atributy, jako například sudý ΩP nebo být lichý ΩJá
Ωp : 2, 4, 6
ΩJá : 1, 3, 5
Které lze definovat jako neelementární atributy.
Příklad
- Chceme vypočítat frekvenci každého možného součtu při hodu dvěma kostkami.
K tomu je naprogramován experiment, kde jsou v každé iteraci přidány dva zdroje náhodných hodnot mezi [1, 6].
Data se zaznamenávají do tabulky a studují se trendy ve velkém počtu.
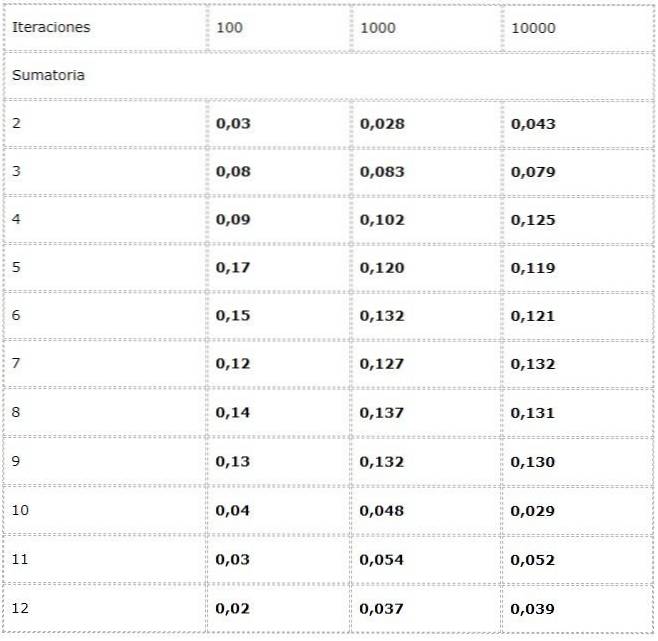
Je pozorováno, že výsledky se mohou mezi iteracemi značně lišit. Zákon velkého počtu však lze vidět ve zjevné konvergenci uvedené v posledních dvou sloupcích.
Reference
- Statistiky a hodnocení důkazů pro forenzní vědce. Druhé vydání. Colin G.G. Aitken. Matematická škola. The University of Edinburgh, UK
- Matematika pro informatiku. Eric Lehman. Google Inc..
F Thomson Leighton Katedra matematiky a výpočetní techniky a laboratoře AI, Massachusetts Institute of Technology; Akamai Technologies - Aritmetický učitel, svazek 29. Národní rada učitelů matematiky, 1981. University of Michigan.
- Učení a výuka teorie čísel: Výzkum poznávání a výuky / editace Stephen R. Campbell a Rina Zazkis. Ablex publishing 88 Post Road West, Westport CT 06881
- Bernoulli, J. (1987). Ars Conjectandi- 4ème partie. Rouen: IREM.



Zatím žádné komentáře