
Teoretická pravděpodobnost, jak ji získat, příklady, cvičení
The teoretická pravděpodobnost (nebo Laplace), že dojde k události E, která patří do vzorového prostoru S, ve kterém mají všechny události stejnou pravděpodobnost výskytu, je definována v matematické notaci jako: P (E) = n (E) / N (S)
Kde P (E) je pravděpodobnost, daná jako podíl mezi celkovým počtem možných výsledků události E, kterou nazýváme n (E), vydělená celkovým počtem N (S) možných výsledků ve vzorovém prostoru S.

Teoretická pravděpodobnost je reálné číslo mezi 0 a 1, ale často se vyjadřuje v procentech, v takovém případě bude pravděpodobností hodnota mezi 0% a 100%.
Výpočet pravděpodobnosti výskytu události je velmi důležitý v mnoha oblastech, jako je obchodování, pojišťovny, hazardní hry a mnoho dalších..
Rejstřík článků
- 1 Jak získat teoretickou pravděpodobnost?
- 2 Příklady
- 2.1 Příklad 1
- 2.2 Příklad 2
- 3 cvičení
- 3.1 Cvičení 1
- 3.2 Cvičení 2
- 3.3 Cvičení 3
- 3.4 Cvičení 4
- 4 Odkazy
Jak získat teoretickou pravděpodobnost?
Názorným případem je případ tomboly nebo loterie. Předpokládejme, že je vydáno 1 000 lístků na losování smartphonu. Vzhledem k tomu, že losování probíhá náhodně, má kterákoli z tiketů stejnou šanci stát se vítězem.
Chcete-li zjistit pravděpodobnost, že vyhraje osoba, která si koupí tiket s číslem 81, použijte následující výpočet teoretická pravděpodobnost:
P (1) = 1/1 000 = 0,001 = 0,1%
Předchozí výsledek je interpretován následovně: pokud by se losování opakovalo nekonečně mnohokrát, každých 1 000krát by byl vybrán tiket 81, v průměru jednou.
Pokud někdo z nějakého důvodu získá všechny lístky, je jisté, že cenu vyhraje. Pravděpodobnost výhry, pokud máte všechny tikety, se počítá takto:
P (1 000) = 1 000/1 000 = 1 = 100%.
To znamená, že pravděpodobnost 1 nebo 100% znamená, že je zcela jisté, že k tomuto výsledku dojde..
Pokud někdo vlastní 500 tiketů, šance na výhru nebo prohru jsou stejné. Teoretická pravděpodobnost výhry ceny se v tomto případě počítá takto:
P (500) = 500/1 000 = ½ = 0,5 = 50%.
Ten, kdo si nekoupí žádný tiket, nemá šanci na výhru a jeho teoretická pravděpodobnost se určuje následovně:
P (0) = 0/1 000 = 0 = 0%
Příklady
Příklad 1
Máte minci s drahý na jedné straně a štít nebo razítko na druhé straně. Jaká je teoretická pravděpodobnost, že když je mince hodena, objeví se v hlavě??
P (drahý) = n (drahý) / N ( obličej + štít ) = ½ = 0,5 = 50%
Výsledek je interpretován následovně: pokud by bylo provedeno velké množství losování, v průměru v každém 2 losování by jeden z nich narazil do hlavy.
V procentech je interpretace výsledku taková, že provedení nekonečně velkého počtu losování, v průměru ze 100 z nich 50 by mělo za následek.
Příklad 2
V krabici jsou 3 modré kuličky, 2 červené kuličky a 1 zelený. Jaká je teoretická pravděpodobnost, že když vytáhnete mramor z krabice, bude červený?
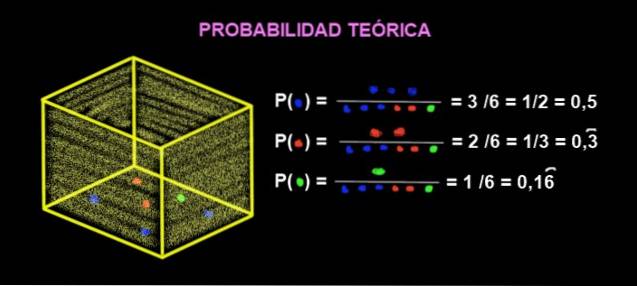
Pravděpodobnost, že to vyjde červeně, je:
P (červená) = počet příznivých případů / počet možných případů
A to:
P (červená) = počet červených kuliček / celkový počet kuliček
A konečně, pravděpodobnost, že se nakreslí červený mramor, je:
P (červená) = 2/6 = ⅓ = 0,3333 = 33,33%
Zatímco pravděpodobnost, že při kreslení zeleného mramoru je:
P (zelená) = ⅙ = 0,1666 = 16,66%
Teoretická pravděpodobnost získání modrého mramoru při slepé těžbě je:
P (modrá) = 3/6 = ½ = 0,5 = 50%
To znamená, že za každé 2 pokusy bude výsledek modrý v jednom z nich a další barva v dalším pokusu, za předpokladu, že je extrahovaný mramor nahrazen a že počet pokusů je velmi, velmi velký..
Výcvik
Cvičení 1
Určete pravděpodobnost, že při válcování kostkou bude získána hodnota menší nebo rovna 4.
Řešení
Pro výpočet pravděpodobnosti výskytu této události bude použita definice teoretické pravděpodobnosti:
P (≤4) = počet příznivých případů / počet možných případů
P (≤5) = 5/6 = = 83,33%
Cvičení 2
Najděte pravděpodobnost, že při dvou po sobě jdoucích hodech normální šestistranné kostky se 5 hodí 2krát.
Řešení
K zodpovězení tohoto cvičení je vhodné vytvořit tabulku, která ukazuje všechny možnosti. První číslice označuje výsledek první kostky a druhá výsledek druhé.
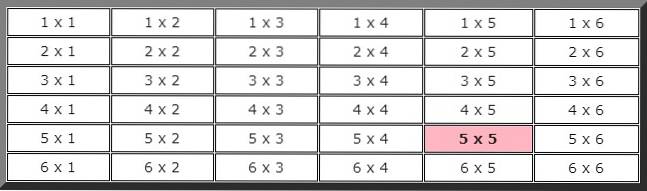
Pro výpočet teoretické pravděpodobnosti potřebujeme znát celkový počet možných případů, v tomto případě, jak je patrné z předchozí tabulky, existuje 36 možností.
Rovněž podle tabulky lze odvodit, že počet případů příznivých pro případ, že při dvou po sobě následujících vypuštěních vyjde 5, je pouze 1, zvýrazněný barvou, proto je pravděpodobnost, že k této události dojde:
P (5 x 5) = 1/36.
Tohoto výsledku bylo možné dosáhnout také pomocí jedné z vlastností teoretické pravděpodobnosti, která uvádí, že kombinovaná pravděpodobnost dvou nezávislých událostí je výsledkem jejich individuálních pravděpodobností..
V tomto případě je pravděpodobnost, že první losování bude hodit 5, je ⅙. Druhé losování je zcela nezávislé na prvním, proto je pravděpodobnost, že se v druhém hodí 5, také ⅙. Kombinovaná pravděpodobnost tedy je:
P (5 × 5) = P (5) P (5) = (1/6) (1/6) = 1/36.
Cvičení 3
Najděte pravděpodobnost, že se při prvním losování hodí číslo menší než 2 a při druhém se hodí číslo větší než 2.
Řešení

Opět musí být vytvořena tabulka možných událostí, kde jsou zvýrazněny ty, ve kterých byl první hod menší než 2 a ve druhém větší než 2..
Celkově existují 4 možnosti z celkem 36. To znamená, že pravděpodobnost této události je:
P (<2 ; >2) = 4/36 = 1/9 = 0,1111 = 11,11%
Pomocí věty o pravděpodobnosti, která uvádí:
Pravděpodobnost výskytu dvou nezávislých událostí se rovná součinu jednotlivých pravděpodobností.
Získá se stejný výsledek:
P (<2) P(>2) = (1/6) (4/6) = 4/36 = 0,1111 = 11,11%
Hodnota získaná tímto postupem se shoduje s předchozím výsledkem prostřednictvím teoretické nebo klasické definice pravděpodobnosti.
Cvičení 4
Jaká je pravděpodobnost, že při hodu dvěma kostkami je součet hodnot 7.
Řešení

Pro nalezení řešení v tomto případě byla vypracována tabulka možností, ve kterých byly barevně označeny případy, které splňují podmínku, že součet hodnot bude 7.
Při pohledu na tabulku lze spočítat 6 možných případů, takže pravděpodobnost je:
P (I + II: 7) = 6/36 = 1/6 = 0,1666 = 16,66%
Reference
- Canavos, G. 1988. Pravděpodobnost a statistika: Aplikace a metody. Mcgraw kopec.
- Devore, J. 2012. Pravděpodobnost a statistika pro inženýrství a vědu. 8. Edice. Cengage.
- Lipschutz, S. 1991. Schaum Series: Probability. Mcgraw kopec.
- Obregón, I. 1989. Teorie pravděpodobnosti. Redakční Limusa.
- Walpole, R. 2007. Pravděpodobnost a statistika pro strojírenství a vědy. Pearson.



Zatím žádné komentáře