Přidružení asociativních vlastností, násobení, příklady, cvičení

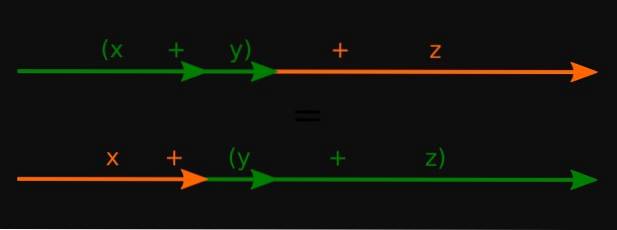
The asociativní majetek součtu představuje asociativní charakter operace součtu v různých matematických množinách. V něm jsou příbuzné tři (nebo více) prvků těchto sad, které se nazývají a, bac, takže vždy platí:

a + (b + c) = (a + b) + c

Tímto způsobem je zaručeno, že bez ohledu na způsob seskupení k provedení operace je výsledek stejný.

Je však třeba poznamenat, že asociativní vlastnost není synonymem komutativní vlastnosti. To znamená, že víme, že pořadí sčítání nemění součet nebo že pořadí faktorů nemění produkt. Takže pro součet to lze zapsat takto: a + b = b + a.

V asociativní vlastnosti je to však jiné, protože je zachováno pořadí prvků, které mají být přidány, a jaké změny jsou provedeny jako první. Což znamená, že nezáleží na tom přidat první (b + c) a k tomuto výsledku přidat a, než začít přidávat a s b a do výsledku přidat c.

Mnoho důležitých operací, jako je přidání, je asociativních, ale ne všechny. Například při odečítání reálných čísel se stane, že:

a - (b - c) ≠ (a - b) - c

Pokud a = 2, b = 3, c = 1, pak:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

Rejstřík článků

• 1 Asociativní vlastnost násobení
  • 1.1 Aplikace asociativní vlastnosti násobení
• 2 Příklady
  • 2.1 Asociativní vlastnost ve vektorech
  • 2.2 Faktorizace polynomů seskupením termínů
• 3 cvičení
  • 3.1 - Cvičení 1
  • 3.2 - Cvičení 2
• 4 Odkazy

Asociativní vlastnost násobení

Jak bylo provedeno pro přidání, asociativní vlastnost násobení uvádí, že:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

V případě množiny reálných čísel lze snadno ověřit, že tomu tak vždy je. Například pomocí hodnot a = 2, b = 3, c = 1 máme:

dva _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

Reálná čísla splňují asociativní vlastnost sčítání i násobení. Na druhou stranu v jiné sadě, jako je například vektor, je součet asociativní, ale křížový součin nebo vektorový součin nikoli..

Aplikace asociativní vlastnosti násobení

Výhodou operací, ve kterých je asociativní vlastnost splněna, je schopnost seskupovat nejvhodnějším způsobem. Díky tomu je rozlišení mnohem jednodušší..

Předpokládejme například, že v malé knihovně jsou 3 police, každá s 5 policemi. V každé polici je 8 knih. Kolik knih je celkem?

Můžeme provést operaci takto: celkový počet knih = (3 x 5) x 8 = 15 x 8 = 120 knih.

Nebo takto: 3 x (5 x 8) = 3 x 40 = 120 knih.

Příklady

-V množinách přirozených, celých, racionálních, reálných a komplexních čísel jsou splněny asociativní vlastnosti sčítání a násobení.

-Pro polynomy také platí v těchto operacích.

-V případě operací odčítání, dělení a umocňování není asociativní vlastnost splněna ani v reálných číslech, ani v polynomech.

-V případě matic platí asociativní vlastnost pro sčítání a násobení, i když v druhém případě není komutativita splněna. To znamená, že vzhledem k maticím A, B a C platí, že:

(A x B) x C = A x (B x C)

Ale ... A x B ≠ B x A

Asociativní vlastnost ve vektorech

Vektory tvoří jinou množinu než reálná čísla nebo komplexní čísla. Operace definované pro sadu vektorů jsou poněkud odlišné: existují sčítání, odčítání a tři typy produktů.

Součet vektorů splňuje asociativní vlastnost, stejně jako čísla, polynomy a matice. Co se týče skalárních součinů, skalárních vektorem a křížem, které jsou vytvořeny mezi vektory, druhý jej nesplňuje, ale skalární součin, což je další druh operace mezi vektory, jej splňuje, přičemž zohledňuje následující:

-Produkt skaláru a vektoru má za následek vektor.

-A když skalárně vynásobíme dva vektory, vznikne skalár.

Proto vzhledem k vektorům proti, nebo Y w, a navíc skalární λ, je možné psát:

-Součet vektorů: proti +(nebo + w ) = (proti + nebo) + w

-Skalární součin: λ (proti • nebo ) = (λproti) • nebo

To je možné díky proti • nebo má za následek skalár a λproti je to vektor.

Nicméně:

proti × (nebo × w ) ≠ (proti × nebo)×w

Faktorizace polynomů seskupením termínů

Tato aplikace je velmi zajímavá, protože jak již bylo řečeno, asociativní vlastnost pomáhá řešit určité problémy. Součet monomiálů je asociativní a lze jej použít k výpočtu faktorů, když se na první pohled neobjeví zřejmý společný faktor.

Předpokládejme například, že požádáte o faktor: X³ + dvaX^dva + 3X +6. Tento polynom nemá žádný společný faktor, ale podívejme se, co se stane, pokud bude seskupen takto:

X³ + 2x^dva + 3x +6 = (x³ + 2x^dva) + (3x +6)

První závorka má společný faktor X^dva:

X³ + dvaX^dva = X^dva (x + 2)

Ve druhém je společný faktor 3:

3x +6 = 3 (x + 2)

Pak:

X³ + dvaX^dva + 3X +6 = X^dva(x + 2) + 3 (x + 2)

Nyní existuje zjevný společný faktor, který je x + 2:

X^dva(x + 2) + 3 (x + 2) = (x + 2) (x^dva+3)

Výcvik

- Cvičení 1

Budova školy má 4 patra a v každé je 12 učeben s 30 pracovními stoly uvnitř. Kolik lavic má škola celkem?

Řešení

Tento problém je vyřešen použitím asociativní vlastnosti násobení, pojďme se podívat:

Celkový počet stolů = 4 patra x 12 učeben / patro x 30 stolů / učebna = (4 x 12) x 30 stolů = 48 x 30 = 1440 stolů.

Nebo pokud chcete: 4 x (12 x 30) = 4 x 360 = 1440 stolů

- Cvičení 2

Vzhledem k polynomům:

A (x) = 5x³ + 2x^dva -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x^dva +3x -7

Použijte asociativní vlastnost přidání k vyhledání A (x) + B (x) + C (x).

Řešení

Můžete seskupit první dva a přidat třetí k výsledku:

A (x) + B (x) = [5x³ + 2x^dva -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x^dva -12x +1

Okamžitě je přidán polynom C (x):

[X⁴ + 11x³+ 2x^dva -12x +1] + [-8x^dva +3x -7] = x⁴ + 11x³ - 6x^dva -9x -6

Čtenář si může ověřit, že je výsledek shodný, pokud je vyřešen pomocí možnosti A (x) + [B (x) + C (x)].

Reference

1. Jiménez, R. 2008. Algebra. Hala Prentice.
2. Matematika je zábava, komutativní, asociativní a distribuční zákony. Obnoveno z: mathisfun.com.
3. Matematický sklad. Definice asociativního majetku. Obnoveno z: mathwarehouse.com.
4. Vědění. Asociativní a komutativní vlastnost sčítání a násobení (s příklady). Obnoveno z: sciencing.com.
5. Wikipedia. Asociativní vlastnost. Obnoveno z: en.wikipedia.org.