
Válcové projekční charakteristiky, výhody a nevýhody
The válcová projekce v kartografii je to ten, ve kterém jsou body na kulovém povrchu promítnuty na válec, jehož osa se shoduje s přímkou, která prochází póly a je tečna nebo sečna ke kouli. Válec je povrch, který lze otevřít v rovině tvořící obdélník, aniž by na něj promítané čáry utrpěly deformaci.
Existuje několik válcových projekcí, ve kterých se rovnoběžky stávají vodorovnými čarami a poledníky svislými čarami, jakmile je válec vysunut v rovině. Obecně je projekční válec zvolen tak, aby byl tečný k rovníkové linii Země. V tomto případě se jeho poloměr bude rovnat poloměru rovníku, viz obrázek 1.
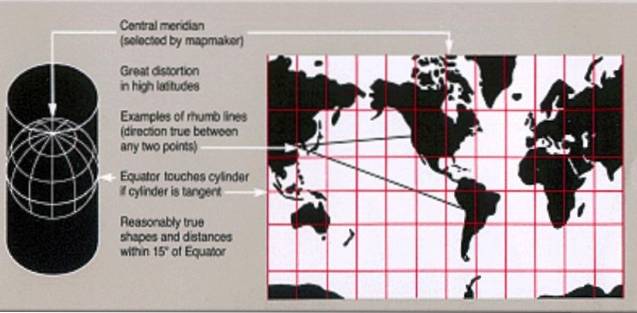
Lze však také zvolit projekční válce, které se sečou ke dvěma rovnoběžkám ve stejné vzdálenosti od rovníkové čáry, v tomto případě bude mít válec poloměr menší než rovníkový poloměr.
Výsledná mapa válcového průmětu poté představí mřížku vodorovných rovnoběžek a svislých poledníků tvořících pravé úhly..
Rejstřík článků
- 1 Výhody válcového výstupku
- 1.1 Válcová Mercatorova projekce
- 2 Nevýhody
- 2.1 Válcová webová projekce - Mercator
- 2.2 Válcová Lambertova projekce
- 3 Jiné typy válcových výstupků, jejich silné a slabé stránky
- 3.1 Equidistant válcový výstupek
- 3.2 Válcová Millerova projekce
- 4 Odkazy
Výhody válcového výstupku
V kartografii se používá několik typů válcových projekcí, z nichž každý má své silné a slabé stránky. V každém případě bude výběr typu projekce záviset na konečném účelu mapy..
Výhodou této i jakékoli další kartografické projekce je, že prostřednictvím nich můžete vizualizovat části Země na rovném povrchu a vzít je s sebou, abyste je mohli snadno konzultovat..
Válcová projekce je velmi vhodná pro mapy světa, protože lze zobrazit obě hemisféry, na rozdíl od jiných projekcí, jako je kuželová projekce, která umožňuje pouze reprezentaci jedné z hemisfér.
Nyní, když představuje sférický povrch v rovině, bude vždy tak či onak narušen. V případě válcového průmětu dochází k nejmenšímu zkreslení v intertropické zóně.
Právě s cílem využít výhod tohoto typu projekce, ale zároveň se snažit minimalizovat tyto nepříjemnosti, navrhli geografové v průběhu staletí různé typy válcových projekcí..
Válcová Mercatorova projekce
Vynález této projekce je přičítán belgickému kartografovi, geografovi a matematikovi Gerardovi Mercatorovi v roce 1569. Jde o jednu z nejpoužívanějších projekcí na světových mapách i dnes..
Jeho hlavní ctností je, že trasa s konstantním směrem je na mapě znázorněna přímkou.
Kvůli této jedinečné vlastnosti šlo o typ mapy, který navigátoři přijali krátce po vydání. Jedná se pak o konformní projekci, protože zachovává směry a úhly.
Ale právě díky tomu projekce Mercatoru nezachovává oblasti. Regiony mimo tropy a hlavně ty, které jsou velmi na severu nebo na jihu, vypadají přehnaně velké.
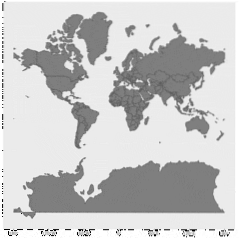
Od svého vzniku se projekce Mercator široce používá k reprezentaci světových map s kontinenty a zeměmi..
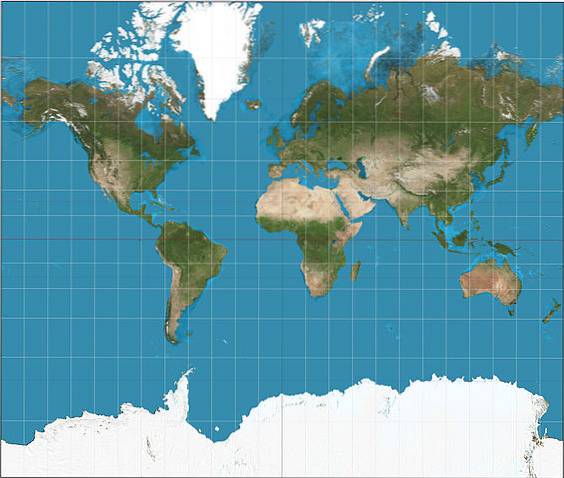
V poslední době se konspirační teorie rozšířila po sociálních sítích, což potvrzuje, že bohaté země mají o tento typ projekcí zájem, aby se na mapě světa objevily větší a silnější než chudé země v tropických oblastech. Tento typ argumentace je naprostý klam.
Nevýhody
Problém s válcovou projekcí, jak jsme viděli v předchozích částech, spočívá v tom, že měřítko je zkreslené směrem od rovníku nebo referenčních rovnoběžek, známých také jako standardní rovnoběžky..
Hlavní nevýhodou je, že mimo intertropické oblasti se toto zkreslení tvarů a vzdáleností zvyšuje, což zvyšuje uvedenou deformaci pro polární šířky, takže tato území vypadají mnohem větší, než ve skutečnosti jsou..
Z tohoto důvodu byly provedeny úpravy, aby se co nejvíce eliminovalo zkreslení, vznikající varianty válcových výstupků, jejichž hlavní charakteristiky jsou uvedeny níže.
Válcová webová projekce - Mercator
Jedná se o variantu klasické projekce Mercator, která se stala standardním mapovacím systémem pro web. Toto je systém, který společnost Google přijala v roce 2005 pro své oblíbené aplikace, Mapy Google a Google Earth..
Tento projekční systém si osvojili další významní poskytovatelé internetových map, jako jsou Bing Maps, Mapquest, OpenStreetMap, Mapbox a další..
Rozdíl mezi původní projekcí Mercator a tímto typem projekce je velmi jemný a konečný výsledek se mění velmi málo..
V původní projekci se Země považuje za kouli, zatímco ve Web - Mercatoru se Země považuje za elipsoidní..
Existují však země, které tato vylepšení ve svých mapách nepřijaly. Například pro kontinentální Spojené státy a Kanadu je pro letecké navigační mapy upřednostňována projekce Lambert Conformal Conic a pro záležitosti katastru projekce Albert Conic..
Válcová Lambertova projekce
Jedná se o válcovou projekci navrženou v roce 1772 švýcarským matematikem a geografem Johann Heinrichem Lambertem (1728-1777). Ve své původní verzi používá Lambert rovníkovou čáru jako referenční paralelu.
U tohoto typu projekce je cílem opravit zkreslení v oblasti zavedené Mercatorovou projekcí, a proto je také známá jako válcová projekce stejné plochy..
Konstance v oblasti Lambertova projekce je dosažena za cenu deformace v tomto aspektu, zejména v oblastech velkých hodnot zeměpisné šířky.
Z tohoto typu projekce vyplynula rodina nejméně sedmi variant, ve které jsou vybrány dvě rovnoběžky ve stejné vzdálenosti od rovníkové čáry, přičemž invariance v oblasti je zachována jako základní charakteristika, ale minimalizuje se deformace v zeměpisných šířkách podle používání mapy.
Jiné typy válcových výstupků, jejich přednosti a vady
Kromě těch, které již byly přezkoumány, existují i jiné typy válcových výčnělků, dokonce docela staré. Některé z nich jsou popsány níže.
Equidistant válcový výstupek
Jedná se o typ jednoduché projekce, ve které se meridiány zemské koule stávají stejně rozmístěnými svislými čarami. Podobným způsobem se rovnoběžky nebo kruhy zeměpisné šířky stávají vodorovnými čarami, které jsou také ve stejné vzdálenosti..
Tento typ projekce je velmi starodávný a připisuje se Marinovi z Tyrios, řeckému geografovi, který žil mezi 70 a 130 n. L. C.
Nevýhodou tohoto typu projekce je, že deformuje oblasti a formy hlavně v zónách zeměpisné šířky vyšších než v tropech, přičemž vodorovně zplošťuje formy v blízkosti polárních oblastí..
Tento typ projekce proto nezachovává oblasti a úhly, s výjimkou rovníkové rovnoběžky, kde je přesná.
Válcová Millerova projekce
Navrhl to kartograf Osborn Maitland Miller (1897-1979) v roce 1942 pomocí rovníku jako standardní paralely projekčního válce..
Tato projekce je velmi podobná projekci Mercator, ale s nevýhodou, že není kompatibilní, to znamená, že fixní kurz na Millerově mapě vypadá jako křivka..
Aby vytvořil svou projekci, Miller vycházel z Mercatorovy projekce, vynásobil skutečnou šířku faktorem ⅘ a poté provedl Mercatorovu projekci. Pro kompenzaci faktoru na projektované zeměpisné šířce se vynásobí inverzním faktorem, tj. 5/4.
Výsledkem je, že formy ve vysokých zeměpisných šířkách ve srovnání s původní formou trpí menším zkreslením..
Reference
- Aguilar, A. 2004. Obecná geografie. 2. místo Edice. Prentice Hall. 57-58.
- Ebrahim Ghaderpour. Projekce mapy. Obnoveno z: researchgate.net
- Gisgeografie. Co jsou mapové projekce? Obnoveno z: gisgeography.com
- Gisgeografie. Válcová projekce. Obnoveno z: gisgeography.com
- Weisstein, E. Válcová projekce. Obnoveno z: mathworld.wolfram.com
- Wikipedia. Lambertova válcová projekce na stejnou plochu. Obnoveno z: en.wikipedia.com
- Wikipedia. Mercatorova projekce. Obnoveno z: en.wikipedia.com
- Wikipedia. Seznam mapových projekcí. Obnoveno z: en.wikipedia.com



Zatím žádné komentáře