The kartografická kuželová projekce Je charakterizován promítáním bodů sférické plochy na povrch kužele, jehož vrchol je umístěn na ose, která prochází póly a je tečna nebo sečna ke kouli. Kužel je povrch, který lze otevřít v rovině, tvořící úhlový sektor a aniž by zdeformoval čáry promítané na něj.
Tuto projekci navrhl matematik Johann Heinrich Lambert (1728 - 1777), který se poprvé objevil ve své knize Freye perspektiva (1759), kde sestavil různé teorie a úvahy o projekcích.
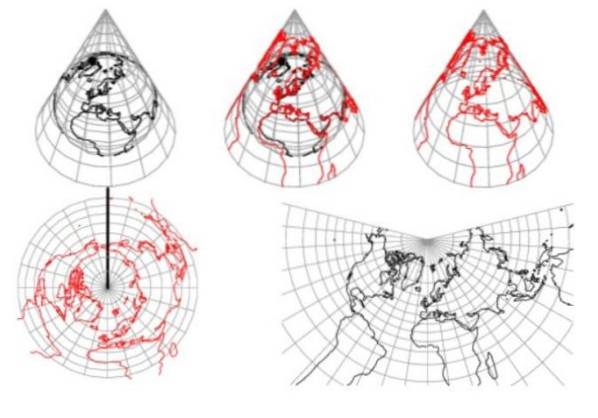
V kuželovitých projekcích zemského povrchu se meridiány stávají radiálními liniemi soustředěnými na vrcholu se stejnými úhlovými rozestupy a pozemské rovnoběžky se stávají kruhovými oblouky soustřednými k vrcholu.
Obrázek 1 ukazuje, že kónický výstupek neumožňuje reprezentovat obě hemisféry. Kromě toho je jasně pozorováno, že vzdálenosti jsou zkresleny směrem od rovnoběžek, které zachycují kužel.
Z těchto důvodů se tento typ projekce používá k reprezentaci oblastí střední šířky, rozsáhlých od východu na západ a menšího rozsahu sever-jih. Tak je tomu v kontinentálních Spojených státech.
Rejstřík článků
Zemi lze přiblížit na kouli o poloměru 6378 km, vzhledem k tomu, že veškerá pevnina a vodní hmoty jsou na této velké kouli. Jde o převod této plochy, která pokrývá objekt ve třech rozměrech, například kouli, na jiný objekt ve dvou rozměrech: plochá mapa. To přináší nepříjemnosti, že zakřivený povrch je zkreslený, když ho chcete promítnout na rovinu.
Mapové projekce, jako je kónická projekce, se snaží tento problém vyřešit s co nejmenší ztrátou přesnosti. Existuje tedy několik možností, jak provést projekci, v závislosti na vlastnostech, které chcete zvýraznit..
Mezi tyto důležité vlastnosti patří vzdálenosti, povrch, úhly a další. Nejlepší způsob, jak je všechny uchovat, je reprezentovat Zemi ve 3D v měřítku. Ale to není vždy praktické.
Přenášet zeměkouli všude není snadné, protože zabírá objem. Rovněž nevidíte celý povrch Země najednou a není možné reprodukovat všechny podrobnosti na zmenšeném modelu..
Dokážeme si představit, že planeta je oranžová, oloupeme oranžovou a rozložíme ji na stůl a pokusíme se rekonstruovat obraz povrchu oranžové. Je jasné, že v průběhu procesu dojde ke ztrátě mnoha informací.
Možnosti projekce jsou následující:
- Promítněte na letadlo nebo
- Na válci, který lze vyvinout jako obdélníkovou rovinu.
- Konečně na kuželu.
Kónický projekční systém má tu výhodu, že je přesný přes rovnoběžky zvolené k zachycení projekčního kužele..
Kromě toho udržuje orientaci podél meridiánů prakticky neporušenou, i když může mírně zkreslit měřítko podél meridiánů pro zeměpisné šířky daleko od standardních nebo referenčních rovnoběžek. Proto je vhodné zastupovat velmi velké země nebo kontinenty.
Je to kónický projekční systém, který původně používal řecký geograf Ptolemaios, který žil mezi lety 100–170 n. L. Později v roce 1745 byl vylepšen.
Často se používá v atlasech oblastí se středními zeměpisnými šířkami. Je vhodný pro zobrazení oblastí s několika stupni zeměpisné šířky, které patří k jedné z rovníkových polokoulí.
V této projekci jsou vzdálenosti skutečné podél meridiánů a ve dvou standardních rovnoběžkách, tj. Rovnoběžkách vybraných k zachycení s kuželem projekce..
V ekvidistantní kuželovité projekci se bod na kouli rozkládá radiálně až do jejího průsečíku s tečnou nebo sečnatým kuželem, přičemž střed koule je středem projekce.
Nevýhody
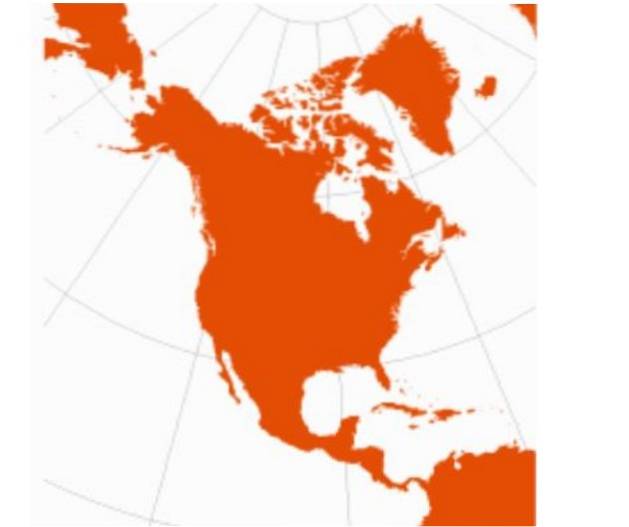
Hlavní nevýhodou kuželovité projekce je, že není použitelná pro rovníkové oblasti.
Kónická projekce navíc není vhodná pro mapování velkých oblastí, ale spíše konkrétních oblastí, jako je Severní Amerika..
Použijte dvě standardní paralely a zachujte oblast, ale ne měřítko a tvar. Tento typ kuželovité projekce zavedl H. C. Albers v roce 1805.
Všechny oblasti na mapě jsou úměrné těm na Zemi. V omezených oblastech jsou směry relativně přesné. Vzdálenosti odpovídají vzdálenostem kulového povrchu na standardních rovnoběžkách.
Ve Spojených státech se tento projekční systém používá pro mapy zobrazující limity států Unie, pro které jsou jako standardní paralely vybrány 29,5 ° N a 45,5 ° N, což má za následek maximální chybu měřítka 1,25%.
Mapy vytvořené pomocí této projekce nezachovávají úhly odpovídající úhlu koule ani nezachovávají perspektivu nebo ekvidistenci.
To bylo navrženo v roce 1772 švýcarským matematikem a geografem stejného jména. Jeho hlavní charakteristikou je, že používá kuželovou tečnu nebo sečnu ke kouli a projekce udržuje úhly neměnné. Díky těmto vlastnostem je velmi užitečný v leteckých navigačních mapách..
Americká geologická služba (USGS) používá projekci Lambert Conic. V této projekci jsou vzdálenosti skutečné podél standardních rovnoběžek.
V Lambertově kuželovité projekci zůstávají směry přiměřeně přesné. Plochy a tvary jsou mírně zkreslené v pozicích blízko standardních rovnoběžek, ale změna tvaru a plochy se zvyšuje s jejich oddělením..
Protože cílem této projekce je udržovat směry a úhly stejné jako ty původní na kouli nebo elipsoidu, neexistuje žádná geometrická metoda jejich získání, na rozdíl od Ptolemaiovy projekce ve stejné vzdálenosti..
Jedná se spíše o analytickou projekční metodu založenou na matematických vzorcích.
Základní mapy USGS pro 48 kontinentálních států používají 33 ° N a 45 ° N jako standardní paralely, což vede k maximální chybě mapy 2,5%..
Pro navigační mapy na Aljašce jsou použité základní rovnoběžky 55 ° N a 65 ° N. Místo toho národní atlas Kanady používá 49 ° N a 77 ° N.
Zatím žádné komentáře