
Mannův U test - Whitney, co to je a kdy se použije, provedení, příklad
The Mann-Whitney U test Používá se pro srovnání dvou nezávislých vzorků, pokud mají málo dat nebo nedodržují normální rozdělení. Tímto způsobem se považuje za test neparametrické, Na rozdíl od svého protějšku Studentův test, který se používá, když je vzorek dostatečně velký a sleduje normální rozdělení.
Frank Wilcoxon to navrhl poprvé v roce 1945 pro vzorky stejné velikosti, ale o dva roky později byl rozšířen pro případ vzorků různých velikostí Henrym Mannem a D. R. Whitneym.
Test se často používá ke kontrole, zda existuje vztah mezi kvalitativní a kvantitativní proměnnou.
Ilustrativním příkladem je odebrání souboru hypertoniků a extrakce dvou skupin, od kterých jsou zaznamenávány údaje o denním krevním tlaku po dobu jednoho měsíce.
Léčba A se aplikuje na jednu skupinu a léčba B se aplikuje na jinou skupinu. Zde je krevní tlak kvantitativní proměnnou a typ léčby je kvalitativní..
Chceme vědět, zda je medián, a nikoli průměr, naměřených hodnot statisticky stejný nebo odlišný, abychom zjistili, zda existuje rozdíl mezi těmito dvěma způsoby léčby. Pro získání odpovědi se použije statistika Wilcoxon nebo Mann-Whitney U test..
Rejstřík článků
- 1 Prohlášení o problému v testu Mann-Whitney U.
- 1.1 Kvalitativní proměnné versus kvantitativní proměnné
- 2 Charakteristika testu Mann Whitney U.
- 2.1 Mann-Whitneyův vzorec
- 2.2 Kroky k provedení zkoušky
- 3 Praktický příklad aplikace
- 3.1 - Krok 1
- 3.2 - Krok 2
- 3.3 Krok 3
- 3.4 Krok 4
- 4 online kalkulačky pro Mannův U test - Whitney
- 5 Reference
Prohlášení o problému v testu Mann-Whitney U.
Další příklad, ve kterém lze test použít, je následující:
Předpokládejme, že chcete vědět, zda se spotřeba nealkoholických nápojů ve dvou regionech země výrazně liší.
Jeden z nich se jmenuje region A a druhý region B. Je veden záznam o litrech spotřebovaných týdně ve dvou vzorcích: jeden z 10 lidí pro region A a další z 5 lidí pro region B.
Data jsou následující:
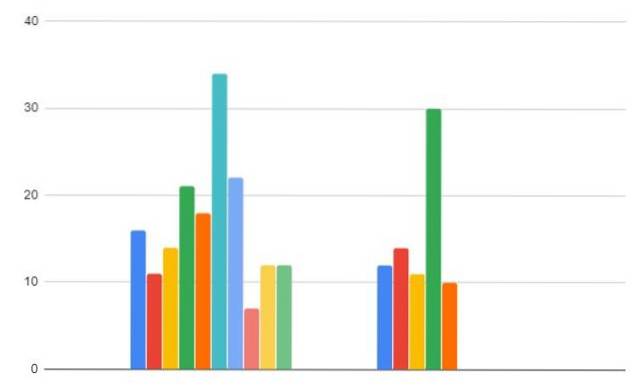
-Region A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12
-Region B: 12,14, 11, 30, 10
Vyvstává následující otázka:
Závisí spotřeba nealkoholických nápojů (Y) na regionu (X)?
Kvalitativní proměnné versus kvantitativní proměnné
-Kvalitativní proměnná X: Region
-Kvantitativní proměnná Y: Spotřeba sody
Pokud je množství spotřebovaného litru v obou regionech stejné, dojde k závěru, že mezi oběma proměnnými neexistuje žádná závislost. Způsob, jak to zjistit, je porovnat průměrný nebo střední trend pro oba regiony.
Normální případ
Pokud data sledují normální rozdělení, vyvstávají dvě hypotézy: nulová H0 a alternativní H1 prostřednictvím srovnání mezi prostředky:
-H0: není žádný rozdíl mezi průměrem obou regionů.
-H1: prostředky obou regionů jsou odlišné.
Případ s neobvyklým trendem
Naopak, pokud data nenásledují normální rozdělení, nebo je vzorek prostě příliš malý na to, aby je znal, místo porovnání průměru by se porovnal medián dvou regionů.
-H0: není žádný rozdíl mezi mediánem obou regionů.
-H1: mediány obou regionů jsou odlišné.
Pokud se mediány shodují, pak je splněna nulová hypotéza: neexistuje žádný vztah mezi konzumací nealkoholických nápojů a regionem.
A pokud se stane opak, alternativní hypotéza je pravdivá: existuje vztah mezi spotřebou a regionem.
Právě pro tyto případy je indikován Mann-Whitneyův U test..
Spárované nebo nepárové vzorky
Další důležitou otázkou při rozhodování, zda použít Mann Whitney U test, je, zda je počet dat v obou vzorcích stejný, to znamená, že jsou na stejné úrovni..
Pokud jsou dva vzorky spárovány, použije se původní verze Wilcoxon. Pokud však ne, jak je tomu v příkladu, použije se modifikovaný Wilcoxonův test, což je přesně Mann Whitney U test..
Vlastnosti testu Mann Whitney U.
Mann-Whitney U test je neparametrický test použitelný na vzorky, které nenásledují normální distribuci nebo s málo daty. Má následující vlastnosti:
1. - Porovnejte mediány
2.- Funguje na objednané rozsahy
3. - Je méně mocná, protože jí síla rozumí pravděpodobnost odmítnutí nulové hypotézy, když je ve skutečnosti nepravdivá.
S přihlédnutím k těmto charakteristikám se test Mann-Whitney U použije, když:
-Data jsou nezávislá
-Nesledují normální rozdělení
-Nulová hypotéza H0 je přijata, pokud se mediány obou vzorků shodují: Ma = Mb
-Alternativní hypotéza H1 je přijata, pokud se mediány obou vzorků liší: Ma ≠ Mb
Mann-Whitneyův vzorec
Proměnná U je statistika kontrastu použitá v Mann-Whitneyově testu a je definována následovně:
U = min (Ua, Ub)
To znamená, že U je nejmenší z hodnot mezi Ua a Ub použitých pro každou skupinu. V našem příkladu by to bylo pro každou oblast: A nebo B..
Proměnné Ua a Ub jsou definovány a počítány podle následujícího vzorce:
Ua = Na Nb + Na (Na +1) / 2 - Ra
Ub = Na Nb + Nb (Nb +1) / 2 - Rb
Zde jsou hodnoty Na a Nb velikosti vzorků odpovídajících oblastem A a B a pro jejich část jsou Ra a Rb hodnostní částky které definujeme níže.
Kroky k provedení testu
1. - Objednejte hodnoty dvou vzorků.
2. - Přiřaďte každé hodnotě pořadí objednávky.
3.- Opravte existující ligatury v datech (opakované hodnoty).
4. - Výpočet Ra = Součet rozsahů vzorku A.
5. - Najít Rb = součet řad vzorků B.
6. - Určete hodnotu Ua a Ub podle vzorců uvedených v předchozí části.
7. - Porovnejte Ua a Ub a menší z nich je přiřazen experimentální statistice U (tj. Dat), která je porovnána s teoretickou nebo normální statistikou U.
Praktický příklad aplikace
Nyní aplikujeme výše uvedené na problém nealkoholických nápojů, které jsme vznesli dříve:
Region A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12
Region B: 12,14, 11, 30, 10
V závislosti na tom, zda jsou prostředky obou vzorků statisticky stejné nebo odlišné, je nulová hypotéza přijata nebo odmítnuta: mezi proměnnými Y a X neexistuje žádný vztah, tj. Spotřeba nealkoholických nápojů nezávisí na regionu:
H0: Ma = Mb
H1: Ma ≠ Mb
- Krok 1
Pokračujeme v objednávání dat společně pro dva vzorky, seřazujeme hodnoty od nejnižší po nejvyšší:

Všimněte si, že hodnota 11 se objeví dvakrát (jednou v každém vzorku). Původně má pozice nebo rozsahy 3 a 4, ale aby nedošlo k nadhodnocení nebo podhodnocení jednoho nebo druhého, jako rozsah se zvolí průměrná hodnota, tj. 3,5.
Podobně postupujeme s hodnotou 12, která se třikrát opakuje s rozsahy 5, 6 a 7.
Hodnotě 12 je přiřazen průměrný rozsah 6 = (5 + 6 + 7) / 3. A totéž pro hodnotu 14, která má ligaturu (objevuje se v obou vzorcích) v pozicích 8 a 9, je jí přiřazen průměrný rozsah 8,5 = (8 + 9) / 2.
- Krok 2
Dále jsou data pro Region A a B znovu oddělena, ale nyní jsou jim odpovídající rozsahy přiřazeny v jiném řádku:
Region A

Region B

Rozsahy Ra a Rb jsou získány ze součtu prvků druhé řady pro každý případ nebo oblast.
Krok 3
Vypočítají se příslušné hodnoty Ua a Ub:
Ua = 10 × 5 + 10 (10 + 1) / 2 - 86 = 19
Ub = 10 × 5 + 5 (5 + 1) / 2-34 = 31
Experimentální hodnota U = min (19, 31) = 19
Krok 4
Předpokládá se, že teoretické U sleduje normální rozdělení N s parametry danými výhradně velikostí vzorků:
N ((na⋅nb) / 2, √ [na nb (na + nb +1) / 12])
Aby bylo možné porovnat experimentálně získanou proměnnou U, s teoretickým U je nutné proměnnou změnit. Přecházíme z experimentální proměnné U na její hodnotu typizovaný, který bude volán Z, aby bylo možné provést srovnání s normalizovaným normálním rozdělením.
Změna proměnné je následující:
Z = (U - na.nb / 2) / √ [na. nb (na + nb + 1) / 12]
Je třeba poznamenat, že pro změnu proměnné byly použity parametry teoretického rozdělení pro U. Potom je nová proměnná Z, která je hybridem mezi teoretickým U a experimentálním U, porovnána se standardizovaným normálním rozdělením N (0 , 1).
Kritéria srovnání
Pokud Z ≤ Zα ⇒ je přijata nulová hypotéza H0
Pokud Z> Zα ⇒ nulová hypotéza H0 je odmítnuta
Standardizované kritické hodnoty Zα závisí na požadované úrovni spolehlivosti, například pro hladinu spolehlivosti α = 0,95 = 95%, což je nejběžnější, kritická hodnota Zα = 1,96.
Pro zde zobrazená data:
Z = (U - na nb / 2) / √ [na nb (na + nb + 1) / 12] = -0,73
Což je pod kritickou hodnotou 1,96.
Konečným závěrem tedy je, že je přijata nulová hypotéza H0:
Mezi regiony A a B není žádný rozdíl ve spotřebě nealkoholických nápojů.
Online kalkulačky pro test Mann - Whitney U.
Existují specifické programy pro statistické výpočty, včetně SPSS a MINITAB, ale tyto programy jsou placené a jejich použití není vždy snadné. Důvodem je skutečnost, že nabízejí tolik možností, že jejich použití je prakticky vyhrazeno odborníkům ve statistice..
Naštěstí existuje několik velmi přesných, bezplatných a snadno použitelných online programů, které vám mimo jiné umožňují spustit Mann-Whitney U test..
Jedná se o tyto programy:
-Social Science Statistics (socscistatistics.com), která má jak Mann-Whitney U test, tak Wilcoxonův test pro případ vyvážených nebo spárovaných vzorků.
-AI Therapy Statistics (ai-therapy.com), která má několik obvyklých testů popisných statistik.
-Statistic to Use (physics.csbsju.edu/stats), jeden z nejstarších, takže jeho rozhraní může vypadat zastaralé, i když se jedná o velmi efektivní bezplatný program.
Reference
- Dietrichson. Kvantitativní metody: hodnostní test. Obnoveno z: bookdown.org
- Průvodce Marínem J. P. SPSS: Analýza a postupy v neparametrických testech. Obnoveno z: halweb.uc3m.es
- USAL MOOC. Neparametrické testy: Mann - Whitney U. Obnoveno z: youtube.com
- Wikipedia. Mann-Whitney U test. Obnoveno z: es.wikipedia.com
- XLSTAT. Centrum nápovědy. Mann - Whitney test tutorial v aplikaci Excel. Obnoveno z: help.xlsat.com



Zatím žádné komentáře