
Co je to magnetický moment?
The magnetický moment je vektor, který souvisí s proudem, který prochází smyčkou nebo uzavřenou smyčkou s její oblastí. Jeho modul se rovná součinu intenzity proudu a plochy a jeho směr a smysl jsou dány pravidlem, jak je znázorněno na obrázku 1.
Tato definice je platná bez ohledu na tvar smyčky. Pokud jde o jednotku magnetického momentu, v mezinárodním systému jednotek SI je to Ampér × mdva.
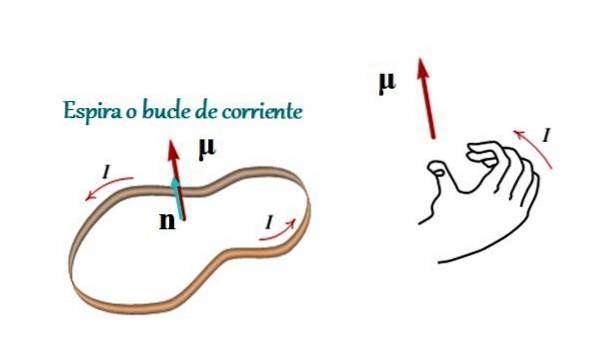
Z matematického hlediska znamená vektor magnetického momentu řeckým písmenem μ (tučně, protože se jedná o vektor, a tím se odlišuje od jeho velikosti), je vyjádřen jako:
μ = AI n
Kde I je intenzita proudu, A je oblast uzavřená smyčkou a n je jednotkový vektor (s modulem rovným 1), který ukazuje ve směru kolmém na rovinu smyčky a jehož smysl je dán pravidlem pravého palce (viz obrázek 1).
Toto pravidlo je velmi jednoduché: zkroucením čtyř prstů pravé ruky, které sledují proud, palec označuje směr a smysl směru. n a tedy magnetického momentu.
Výše uvedená rovnice platí pro smyčku. Pokud existuje N závitů jako v cívce, magnetický moment se vynásobí N:
μ = NAI n
Rejstřík článků
- 1 Magnetický moment a magnetické pole
- 1.1 Magnetické pole dipólu
- 2 Vliv externího pole na smyčku
- 2.1 Točivý moment na obdélníkové smyčce
- 2.2 Potenciální energie magnetického dipólu
- 3 Odkazy
Magnetický moment a magnetické pole
Je snadné najít výrazy pro magnetický moment otáček s pravidelnými geometrickými tvary:
-Čtvercový obrat strany ℓ: μ = Jádva n
-Obdélníková spirála po stranách na Y b: μ = IBA n
-Kruhová spirála o poloměru R: μ = IπRdva n
Dipólové magnetické pole
Magnetické pole produkované smyčkou nebo smyčkou proudu je velmi podobné magnetu tyčového magnetu a také Zemi.
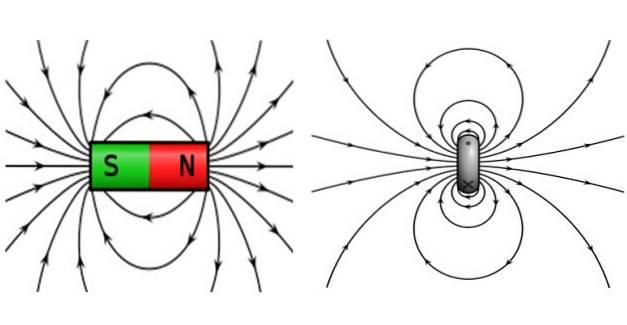
Tyčové magnety se vyznačují tím, že mají severní pól a jižní pól, kde protilehlé póly přitahují a podobné póly odpuzují. Polní čáry jsou uzavřeny, opouštějí severní pól a přicházejí k jižnímu pólu.
Nyní jsou magnetické póly neoddělitelné, což znamená, že pokud rozdělíte tyčový magnet na dva menší magnety, budou mít stále vlastní severní a jižní pól. Není možné mít izolované magnetické póly, proto se nazývá tyčový magnet magnetický dipól.
Magnetické pole kruhové smyčky o poloměru R, nesoucí proud I, se vypočítá pomocí Biot-Savartova zákona. Pro body patřící k jeho ose symetrie (v tomto případě osa x) je pole dáno vztahem:

Vztah mezi magnetickým polem a magnetickým momentem dipólu
Zahrnutí magnetického momentu do výsledků předchozích výrazů:

Tímto způsobem je intenzita magnetického pole úměrná magnetickému momentu. Všimněte si, že intenzita pole klesá s krychlí vzdálenosti.
Tato aproximace je použitelná pro jakoukoli smyčku, pokud X je velký v porovnání se svými rozměry.
A protože čáry tohoto pole jsou tak podobné čarám tyčového magnetu, je rovnice dobrým modelem pro toto magnetické pole a pro ostatní systémy, jejichž čáry jsou podobné, například:
-Nabité částice v pohybu jako elektron.
-Atom.
-Země a další planety a satelity sluneční soustavy.
-Hvězdy.
Vliv externího pole na smyčku
Velmi důležitou charakteristikou magnetického momentu je jeho vazba na točivý moment, který smyčka zažívá v přítomnosti vnějšího magnetického pole..
Elektromotor obsahuje cívky, kterými prochází proud měnícího se směru a které díky vnějšímu poli zažívají spřádací efekt. Tato rotace způsobí pohyb osy a elektrická energie se během procesu převádí na mechanickou energii..
Točivý moment na obdélníkové smyčce
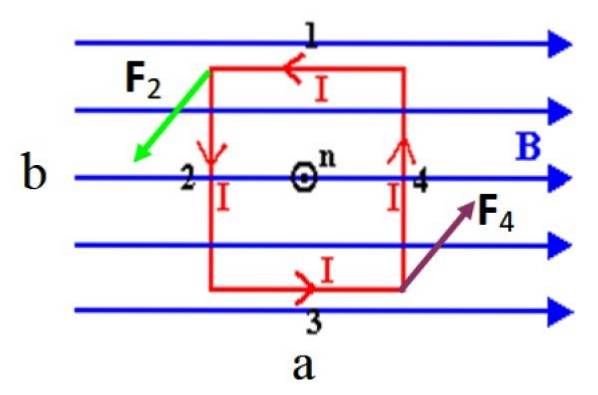
Předpokládejme, pro usnadnění výpočtu, obdélníkovou smyčku se stranami na Y b, jehož normální vektor n, vyčnívající na obrazovku, zpočátku kolmo na rovnoměrné magnetické pole B, jako na obrázku 3. Boky smyčky zažívají síly dané:
F = JáL X B
Kde L je vektor velikosti rovnající se délce segmentu a směrovaný podle proudu, I je jeho intenzita a B je pole. Síla je kolmá na obě L pokud jde o pole, ale ne všechny strany zažívají sílu.

Na obrázku není síla na krátkých stranách 1 a 3, protože jsou rovnoběžné s polem, pamatujte, že součin produktů mezi paralelními vektory je nulový. Avšak dlouhé strany 2 a 4, které jsou kolmé na B, zažít síly označené jako Fdva Y F4.
Tyto síly se tvoří pár: mají stejnou velikost a směr, ale opačné směry, proto nejsou schopny přenášet smyčku uprostřed pole. Ale mohou to otáčet, protože točivý moment τ působící každou silou vzhledem ke svislé ose, která prochází středem smyčky, má stejný směr a smysl.
Podle definice točivého momentu, kde r je poziční vektor:
τ = r X F
Pak:
τdva = τ4=(a / 2) F (+j )
Jednotlivé momenty se nezruší, protože mají stejný směr a smysl, proto se přidají:
τsíť = τdva + τ4 = a F (+j )
Výsledkem je síla F = IbB:
τsíť = I⋅a⋅b⋅B (+j )
Produkt a⋅b je oblast A smyčky, takže Iab je velikost magnetického momentu μ. Proto τsíť = μ⋅B (+j )
Je vidět, že točivý moment se obecně shoduje s vektorovým produktem mezi vektory μ Y B:
τsíť = μ X B
A ačkoli byl tento výraz odvozen od obdélníkové smyčky, je platný pro plochou smyčku libovolného tvaru.
Účinek pole na smyčku je točivý moment, který má tendenci srovnávat magnetický moment s polem.
Potenciální energie magnetického dipólu
Chcete-li otočit smyčku nebo dipól uprostřed pole, je třeba pracovat proti magnetické síle, která mění potenciální energii dipólu. Variace energie ΔU, když se otáčení otáčí z úhlu θnebo úhel θ je dán integrálem:

ΔU = -μB cos θ
Což zase může být vyjádřeno jako bodový produkt mezi vektory B Y μ:
ΔU = - μB
Minimální potenciální energie v dipólu nastává, když cos θ = 1, což znamená, že μ Y B jsou rovnoběžné, energie je maximální, pokud jsou opačné (θ = π) a je nulová, když jsou kolmé (θ = π / 2).
Reference
- Figueroa, D. 2005. Řada: Fyzika pro vědy a inženýrství. Svazek 5. Elektromagnetismus. Upravil Douglas Figueroa (USB).
- Resnick, R. 1999. Fyzika. Sv. 2. 3. vydání. Ve španělštině. Compañía Editorial Continental S.A. autor: C.V.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vyd. 2. díl Pearson.
- Serway, R., Jewett, J. (2008). Fyzika pro vědu a techniku. Svazek 2. 7. Ed. Cengage Learning.
- Tipler, P. (2006) Fyzika pro vědu a technologii. 5. vydání, svazek 2. Redakční reverté.



Zatím žádné komentáře