
Co je elektrická permitivita? (S experimentem)
The elektrická permitivita Je to parametr, který kvantifikuje odezvu média na přítomnost elektrického pole. Označuje se řeckým písmenem ε a jeho hodnota pro prázdnotu, která slouží jako reference pro ostatní média, je následující: εnebo = 8,8541878176 x 10-12 Cdva /N.mdva
Povaha média mu dává zvláštní odezvu na elektrická pole. Tímto způsobem se teplota, vlhkost, molekulová hmotnost, geometrie složek tvořících složek, mechanická napětí v interiéru nebo že v prostoru existuje nějaký preferenční směr, ve kterém je usnadněna existence pole..

V druhém případě se říká, že materiál představuje anizotropie. A když žádný směr není preferenční, materiál je považován izotropní. Propustnost jakéhokoli homogenního média lze vyjádřit jako funkci propustnosti vakua εnebo pomocí výrazu:
ε = κεnebo
Kde κ je relativní propustnost materiálu, nazývaná také dielektrická konstanta, bezrozměrné množství, které bylo experimentálně stanoveno pro mnoho materiálů. Způsob provedení tohoto měření bude vysvětlen později..
Rejstřík článků
- 1 Dielektrika a kondenzátory
- 2 Dielektrikum ve vnějším elektrickém poli
- 3 Měření elektrické permitivity
- 4 Pokus měřit elektrickou permitivitu vzduchu
- 4.1 - Materiály
- 4.2 - Postup
- 5 Reference
Dielektrika a kondenzátory
Dielektrikum je materiál, který nevede dobře elektřinu, takže jej lze použít jako izolátor. To však nebrání tomu, aby materiál byl schopen reagovat na vnější elektrické pole a vytvořit si vlastní..
V následujícím textu budeme analyzovat odezvu izotropních dielektrických materiálů, jako je sklo, vosk, papír, porcelán a některé tuky, které se běžně používají v elektronice..
Mezi dvěma kovovými vrstvami plochého paralelního deskového kondenzátoru lze vytvořit vnější elektrické pole dielektrika..
Dielektrika, na rozdíl od vodičů, jako je měď, postrádají bezplatné náboje, které se mohou v materiálu pohybovat. Jejich základní molekuly jsou elektricky neutrální, ale náboje se mohou mírně posunout. Tímto způsobem je lze modelovat jako elektrické dipóly.
Dipól je elektricky neutrální, ale kladný náboj je oddělen v malé vzdálenosti od záporného náboje. V dielektrickém materiálu a při absenci vnějšího elektrického pole jsou dipóly obvykle náhodně rozloženy, jak je znázorněno na obrázku 2.
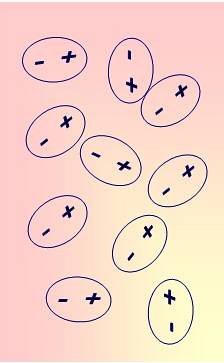
Dielektrikum ve vnějším elektrickém poli
Když je dielektrikum zavedeno uprostřed vnějšího pole, například pole vytvořeného uvnitř dvou vodivých vrstev, dipóly se reorganizují a náboje se oddělí, čímž se vytvoří vnitřní elektrické pole v materiálu v opačném směru než vnější pole..
Když dojde k tomuto posunutí, říká se, že materiál je polarizovaný.
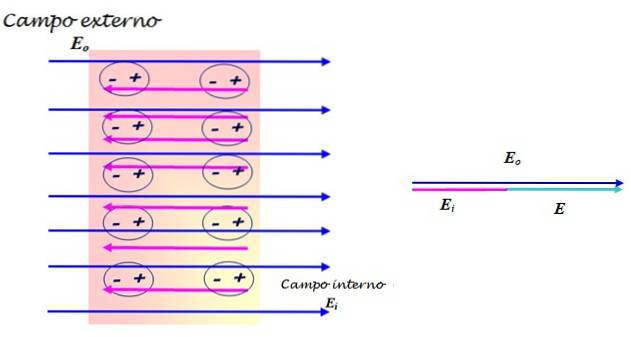
Tato indukovaná polarizace způsobuje síťové nebo výsledné elektrické pole A pokles, účinek znázorněný na obrázku 3, protože vnější pole a vnitřní pole generované uvedenou polarizací, mají stejný směr, ale opačné směry. Velikost A darováno:
E = Enebo - Ai
Vnější pole prochází redukcí díky interakci s materiálem ve faktoru zvaném κ nebo dielektrická konstanta materiálu, což je jeho makroskopická vlastnost. Z hlediska tohoto množství je výsledné nebo čisté pole:
E = Enebo/ κ
Dielektrická konstanta κ je relativní permitivita materiálu, bezrozměrné množství vždy větší než 1 a rovné 1 ve vakuu.
κ = ε/ εnebo
Nebo ε = κεnebo přesně jak bylo popsáno na začátku. Jednotky ε jsou stejné jako jednotky εnebo: Cdva /N.mdva M..
Měření elektrické permitivity
Účinek vložení dielektrika mezi desky kondenzátoru má umožnit uložení dalších nábojů, tj. Zvýšení kapacity. Tuto skutečnost objevil Michael Faraday v 19. století.
Je možné měřit dielektrickou konstantu materiálu pomocí plochého paralelního deskového kondenzátoru následujícím způsobem: když je mezi deskami pouze vzduch, lze ukázat, že kapacita je dána:
Cnebo = εnebo. A / d
Kde Cnebo je kapacita kondenzátoru, NA je plocha desek a d je vzdálenost mezi nimi. Ale když vložíte dielektrikum, kapacita se zvýší o faktor κ, jak je vidět v předchozí části, a pak je nová kapacita C úměrná originálu:
C = κεnebo. A / d = ε. A / d
Poměr mezi konečnou a počáteční kapacitou je dielektrická konstanta materiálu nebo relativní permitivita:
κ = C / Cnebo
A absolutní elektrická permitivita daného materiálu je známa z:
ε = εnebo . (C / Cnebo)
Měření lze snadno provádět, pokud máte multimetr schopný měřit kapacitu. Alternativou je měření napětí Vo mezi deskami kondenzátoru bez dielektrika a izolovaného od zdroje. Poté se zavede dielektrikum a pozoruje se pokles napětí, jehož hodnota bude V.
Pak κ = Vnebo / V
Pokus měřit elektrickou permitivitu vzduchu
-Materiály
- Nastavitelný oddělovací plochý paralelní deskový kondenzátor.
- Mikrometr nebo nonius.
- Multimetr, který má funkci měření kapacity.
- Milimetrový papír.
-Proces
- Vyberte oddělení d mezi deskami kondenzátoru a pomocí multimetru změřit kapacitu Cnebo. Zaznamenejte datový pár do tabulky hodnot.
- Výše uvedený postup opakujte alespoň pro 5 oddělení desek.
- Najděte podíl (A / d) pro každou z měřených vzdáleností.
- Díky výrazu Cnebo = εnebo. A / d je známo, že Cnebo je úměrná kvocientu (A / d). Vyneste každou hodnotu z Cnebo s příslušnou hodnotou A / d.
- Vizuálně upravte nejlepší čáru a určete její sklon. Nebo najděte sklon pomocí lineární regrese. Hodnota sklonu je permitivita vzduchu.
Důležité
Vzdálenost mezi deskami by neměla přesáhnout asi 2 mm, protože rovnice pro kapacitu paralelního plochého kondenzátoru předpokládá nekonečné desky. Je to však docela dobrá aproximace, protože strana desek je vždy mnohem větší než vzdálenost mezi nimi..
V tomto experimentu se určuje permitivita vzduchu, která je velmi blízká vakuu. Dielektrická konstanta vakua je κ = 1, zatímco suchý vzduch je κ = 1 00059.
Reference
- Dielektrický. Dielektrická konstanta. Obnoveno z: electricistas.cl.
- Figueroa, Douglas. 2007. Fyzikální řada pro vědu a techniku. Svazek 5 Elektrické interakce. 2. místo Edice. 213-215.
- Laboratori d'Electricitat ve společnosti Magnetisme (UPC). Relativní propustnost materiálu. Obnoveno z: elaula.es.
- Monge, M. Dielektrika. Elektrostatické pole. University Carlos III v Madridu. Obnoveno z: ocw.uc3m.es.
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14th. Vydání 797 - 806.



Zatím žádné komentáře