
Šikmé charakteristické čáry, rovnice a příklady
The šikmé čáry Jsou to ty, které jsou nakloněné, buď s ohledem na rovný povrch, nebo na jinou přímku, která označuje konkrétní směr. Jako příklad zvažte tři čáry nakreslené v rovině, které se objevují na následujícím obrázku.
Známe jejich relativní polohy, protože je porovnáváme s referenční linií, kterou je obvykle Osa X. označující horizontálu.
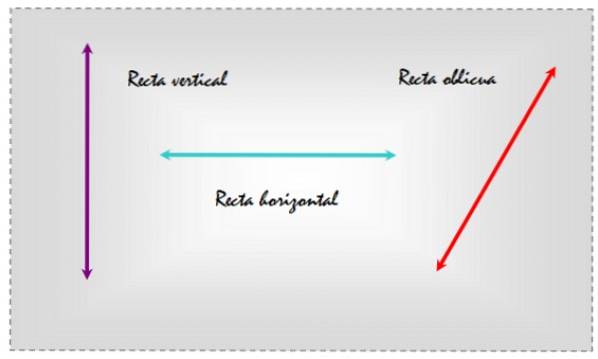
Tímto způsobem, při výběru horizontály jako reference, je čára vlevo svislá, středová vodorovná a pravá šikmá, protože je nakloněna vzhledem k běžným referenčním čarám..
Nyní čáry, které jsou ve stejné rovině, jako je povrch papíru nebo obrazovka, zabírají odlišně relativní polohy navzájem, podle toho, zda se protínají. V prvním případě jsou to sečnaté čáry, zatímco ve druhém jsou rovnoběžné.
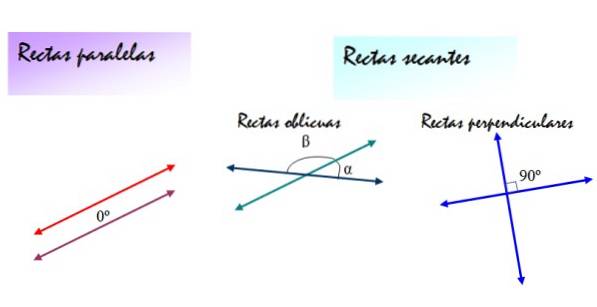
Na druhé straně mohou být sečnickými čarami šikmé čáry nebo kolmé čáry. V obou případech jsou sklony čar přímky odlišné, ale šikmé čáry mezi nimi tvoří úhly α a β, odlišné od 90 °, zatímco úhly určené svislými čarami jsou vždy 90 °..
Následující obrázek shrnuje tyto definice:
Rejstřík článků
- 1 Rovnice
- 1.1 Rovnice přímky v rovině
- 2 Příklady šikmých čar
- 2.1 Paprsky světla
- 2.2 Čáry, které nejsou ve stejné rovině
- 3 Odkazy
Rovnice
Chcete-li znát relativní polohy úseček v rovině, je nutné znát úhel, který mezi sebou tvoří. Řádky jsou:
Paralelní: pokud mají stejný sklon (stejný směr) a nikdy se neprotínají, proto jsou jejich body ve stejné vzdálenosti.
Shodou okolností: když se všechny jeho body shodují, a proto mají stejný sklon, ale vzdálenost mezi jeho body je nulová.
Sušení: pokud jsou jejich svahy odlišné, vzdálenost mezi jejich body se mění a průsečík je jediný bod.
Takže jedním ze způsobů, jak zjistit, zda jsou dvě přímky v rovině sečnatelné nebo rovnoběžné, je jejich sklon. Kritéria rovnoběžnosti a kolmosti čar jsou následující:
Nechť L jsou dva řádky1 a L.dva náležející k rovině, jejíž sklon je m1 a mdva. Tyto řádky jsou rovnoběžné, pokud m1 = mdva a jsou kolmé, když m1= -1 / mdva
Pokud při znalosti sklonů dvou přímek v rovině není splněno žádné z předchozích kritérií, dojde se k závěru, že přímky jsou šikmé. Znát dva body přímky, sklon se vypočítá okamžitě, jak uvidíme v další části.
Je možné zjistit, zda jsou dvě přímky sečnatelné nebo rovnoběžné, a to tak, že najdeme jejich průnik a vyřešíme systém rovnic, které vytvářejí: pokud existuje řešení, jsou to secanty, pokud neexistuje řešení, jsou rovnoběžné, ale pokud jsou řešení nekonečné, řádky jsou shodné.
Toto kritérium nás však neinformuje o úhlu mezi těmito čarami, i když se protínají.
Abychom poznali úhel mezi řádky, jsou zapotřebí dva vektory nebo Y proti které patří každému z nich. Je tedy možné znát úhel, který tvoří pomocí skalárního součinu vektorů, definovaného tímto způsobem:
nebo•v =u.v.cos α
Rovnice přímky v rovině
Přímku v kartézské rovině lze znázornit několika způsoby, například:
-Směrnicový tvar: Ano m je sklon přímky a b je průsečík přímky se svislou osou, rovnice přímky je y = mx + b.
-Obecná rovnice pro přímku: Axe + By + C = 0, kde m = A / B je sklon.
V karteziánské rovině jsou vertikální a horizontální čáry konkrétními případy rovnice přímky.
-Svislé čáry: x = a
-Vodorovné čáry: y = k
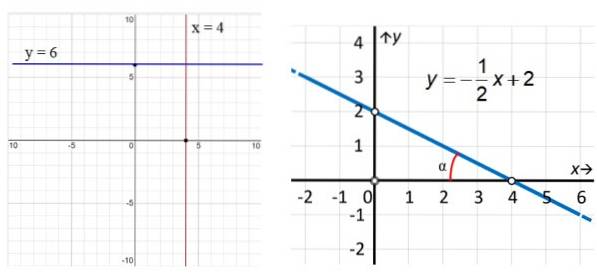
V příkladech na obrázku 3 má svislá červená čára rovnici x = 4, zatímco čára rovnoběžná s osou x (modrá) má rovnici y = 6. Pokud jde o přímku vpravo, vidíme, že je šikmá a najít jeho rovnici použijeme body zvýrazněné na obrázku: (0,2) a (4,0) tímto způsobem:
m = (adva - Y1) / (Xdva - X1) = (2 - 0) / (0 - 4) = - ½
Řez této čáry se svislou osou je y = 2, jak je patrné z grafu. S touto informací:
y = (-½) x + 2
Určení úhlu sklonu vzhledem k ose x je snadné. Cítím to:
α = arctg (2/4) = 26,6 °
Proto je kladný úhel od osy x k přímce: 180 ° - 26,6 ° = 153,4 °
Příklady šikmých čar

Na mnoha místech se objevují šikmé čáry, je třeba věnovat pozornost jejich hledání v architektuře, sportu, elektroinstalaci, potrubí a mnoha dalších místech. V přírodě jsou také přítomny šikmé čáry, jak uvidíme níže:
Paprsky světla
Sluneční světlo se pohybuje po přímce, ale zaoblený tvar Země ovlivňuje to, jak sluneční světlo dopadá na povrch..
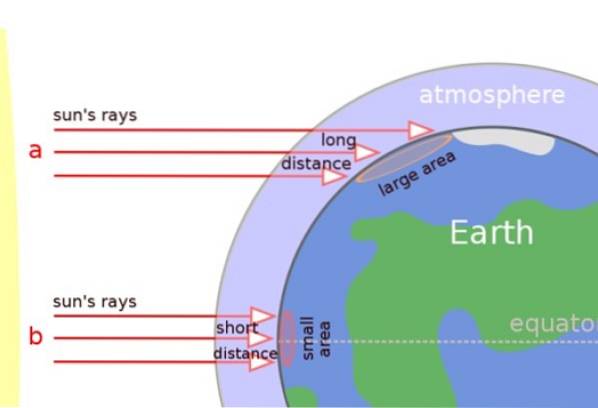
Na obrázku níže jasně vidíme, že sluneční paprsky dopadají kolmo v tropických oblastech, ale v oblastech s mírným podnebím a na pólech se šikmo dostávají na povrch..
Proto sluneční paprsky cestují atmosférou na delší vzdálenost a teplo se také šíří po větší ploše (viz obrázek). Výsledkem je, že oblasti v blízkosti pólů jsou chladnější.
Řádky, které nejsou ve stejné rovině
Pokud dvě čáry nejsou ve stejné rovině, mohou být stále šikmé nebo pokřivený, jak jsou také známé. V tomto případě nejsou jejich směrové vektory paralelní, ale protože nepatří do stejné roviny, neprotínají se tyto čáry.
Například čáry na obrázku 6 vpravo jsou jasně v různých rovinách. Když se na ně podíváte shora, uvidíte, že se skutečně protínají, ale nemají společný bod. Vpravo vidíme kola jízdního kola, jejichž paprsky se při pohledu zepředu zdánlivě protínají.

Reference
- Geometrie. Ředitel vektor čáry. Obnoveno z: juanbragado.es.
- Larson, R. 2006. Kalkul s analytickou geometrií. 8. Edice. Mcgraw kopec.
- Matematika je hra. Čáry a úhly. Obnoveno z: juntadeandalucia.es.
- Přímky, které se protínají. Obnoveno z: profesoraltuna.com.
- Villena, M. Analytical Geometry in R3. Obnoveno z: dspace.espol.edu.ec.
Zatím žádné komentáře