A empirické pravidlo Je výsledkem praktických zkušeností a pozorování v reálném životě. Například je možné vědět, které druhy ptáků lze na určitých místech v každém ročním období pozorovat, a z tohoto pozorování lze stanovit „pravidlo“, které popisuje životní cykly těchto ptáků.
Ve statistikách empirické pravidlo odkazuje na způsob, jakým jsou pozorování seskupena kolem centrální hodnoty, průměru nebo průměru, v jednotkách standardní odchylky..
Předpokládejme, že máte skupinu lidí s průměrnou výškou 1,62 metru a směrodatnou odchylkou 0,25 metru, pak by vám empirické pravidlo umožnilo definovat například, kolik lidí by bylo v intervalu střední plus nebo minus jedna standardní odchylka?
Podle pravidla je 68% dat víceméně jedna standardní odchylka od průměru, to znamená, že 68% lidí ve skupině bude mít výšku mezi 1,37 (1,62-0,25) a 1,87 (1,62 + 0,25) metrů.
Rejstřík článků
Empirické pravidlo je zobecněním Tchebyshevovy věty a normálního rozdělení.
Tchebyshevova věta říká, že: pro určitou hodnotu k> 1 je pravděpodobnost, že náhodná proměnná spadá mezi střední mínus k krát standardní odchylka, a střední plus k krát, standardní odchylka je větší nebo rovna (1 - 1 / kdva).
Výhodou této věty je, že platí pro diskrétní nebo spojité náhodné proměnné s libovolným rozdělením pravděpodobnosti, ale pravidlo z ní definované není vždy velmi přesné, protože závisí na symetrii rozdělení. Čím více bude distribuce náhodné proměnné zkosená, tím méně bude její chování upraveno.
Empirické pravidlo definované z této věty je:
Pokud k = √2, říká se, že 50% dat je v intervalu: [µ - √2 s, µ + √2 s]
Pokud k = 2, říká se, že 75% dat je v intervalu: [µ - 2 s, µ + 2 s]
Pokud k = 3, říká se, že 89% dat je v intervalu: [µ - 3 s, µ + 3 s]
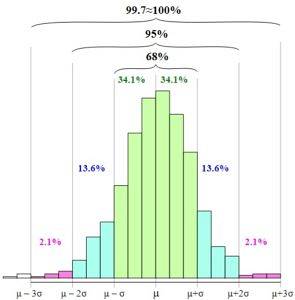
Normální rozdělení, neboli Gaussův zvon, umožňuje stanovit empirické pravidlo nebo pravidlo 68 - 95 - 99,7.
Pravidlo je založeno na pravděpodobnosti výskytu náhodné proměnné v intervalech mezi střední mínus jedna, dvě nebo tři standardní odchylky a střední plus jedna, dvě nebo tři standardní odchylky..
Empirické pravidlo definuje následující intervaly:
68,27% dat je v intervalu: [µ - s, µ + s]
95,45% dat je v intervalu: [µ - 2s, µ + 2s]
99,73% dat je v intervalu: [µ - 3s, µ + 3s]
Na obrázku vidíte, jak jsou tyto intervaly prezentovány a vztah mezi nimi při zvětšování šířky základny grafu.
Proto použití empirického pravidla v měřítku standardní normální proměnné z definuje následující intervaly:
68,27% dat je v intervalu: [-1, 1]
95,45% dat je v intervalu: [-2, 2]
99,73% dat je v intervalu: [-3, 3]
Empirické pravidlo umožňuje zkrácené výpočty při práci s normálním rozdělením.
Předpokládejme, že skupina 100 studentů univerzity má průměrný věk 23 let se standardní odchylkou 2 roky. Jaké informace empirické pravidlo umožňuje?
Uplatnění empirického pravidla zahrnuje následující kroky:
Protože průměr je 23 a směrodatná odchylka 2, pak jsou intervaly:
[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]
[µ - 2 s, µ + 2 s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]
[µ - 3 s, µ + 3 s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]
(100) * 68,27% = přibližně 68 studentů
(100) * 95,45% = přibližně 95 studentů
(100) * 99,73% = přibližně 100 studentů
Nejméně 68 studentů je ve věku od 21 do 25 let.
Nejméně 95 studentů je ve věku od 19 do 27 let.
Téměř 100 studentů je ve věku 17 až 29 let.
Empirické pravidlo je rychlý a praktický způsob, jak analyzovat statistické údaje a je stále spolehlivější, jak se distribuce blíží symetrii.
Jeho užitečnost závisí na oblasti, ve které se používá, a na položených otázkách. Je velmi užitečné vědět, že výskyt hodnot tří směrodatných odchylek pod nebo nad průměrem je téměř nepravděpodobný, dokonce i pro jiné než normální distribuční proměnné je nejméně 88,8% případů v intervalu tří sigma.
Ve společenských vědách je obecně přesvědčivým výsledkem interval střední plus nebo minus dvě sigma (95%), zatímco ve fyzice částic vyžaduje nový efekt považovat za objev interval pěti sigma (99,99994%)..
Odhaduje se, že v přírodní rezervaci žije průměrně 16 000 králíků se standardní odchylkou 500 králíků. Není-li distribuce proměnné „počet králíků v rezervě“ známa, je možné odhadnout pravděpodobnost, že populace králíků je mezi 15 000 a 17 000 králíků?
Interval může být uveden v těchto termínech:
15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s
17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s
Proto: [15000, 17000] = [µ - 2 s, µ + 2 s]
Při použití Tchebyshevovy věty existuje pravděpodobnost minimálně 0,75, že populace králíků v přírodní rezervaci je mezi 15 000 a 17 000 králíků..
Průměrná hmotnost ročních dětí v zemi se obvykle rozdělí na průměr 10 kilogramů a směrodatnou odchylku přibližně 1 kilogram.
a) Odhadněte procento ročních dětí v zemi, které mají průměrnou váhu mezi 8 a 12 kilogramy.
8 = 10 - 2 = 10 - 2 (1) = µ - 2 s
12 = 10 + 2 = 10 + 2 (1) = µ + 2 s
Proto: [8, 12] = [µ - 2s, µ + 2s]
Podle empirického pravidla lze konstatovat, že 68,27% ročních dětí v zemi má váhu mezi 8 a 12 kilogramy.
b) Jaká je pravděpodobnost nalezení jednoročního dítěte o hmotnosti 7 kilogramů nebo méně?
7 = 10 - 3 = 10 - 3 (1) = µ - 3 s
Je známo, že 7 kilogramů hmotnosti představuje hodnotu µ - 3 s, stejně jako je známo, že 99,73% dětí má hmotnost mezi 7 a 13 kilogramy. To ponechává extrémy pouze 0,27% z celkového počtu dětí. Polovina z nich, 0,135%, má 7 kilogramů nebo méně a druhá polovina, 0,135%, má 11 kilogramů nebo více.
Lze tedy dojít k závěru, že existuje pravděpodobnost 0,00135, že dítě váží 7 kilogramů nebo méně.
c) Pokud populace země dosáhne 50 milionů obyvatel a roční děti budou představovat 1% populace země, kolik ročních dětí bude vážit mezi 9 a 11 kilogramy?
9 = 10 - 1 = µ - s
11 = 10 + 1 = µ + s
Proto: [9, 11] = [µ - s, µ + s]
Podle empirického pravidla je v zemi 68,27% ročních dětí v intervalu [µ - s, µ + s]
V zemi žije 500 000 jednoročních dětí (1% z 50 milionů), takže 341 350 dětí (68,27% z 500 000) váží mezi 9 a 11 kilogramy.
Zatím žádné komentáře