Odčítání vektorové grafické metody, příklady, cvičení

The vektorové odčítání nebo vektorové odčítání mezi vektory nebo Y proti označeno nebo - proti, se vypočítá přidáním vektoru nebo s vektorem naproti proti. Algebraicky je odčítání vyjádřeno takto:

nebo - proti = nebo + (-proti)

Je možné provést vektorový odčítání pomocí různých postupů, například graficky, tímto způsobem vektor proti je nakresleno orientovaným úsečkovým segmentem - šipkou-.

Délka šipky odpovídá modulu vektoru, sklon - vzhledem k dané referenční přímce - označuje směr a konec označuje směr vektoru.

Vektor naproti proti má stejnou délku a směr, ale opačný směr. Pak před provedením odečtení mezi nebo Y proti, je nutné nakreslit vektor naproti proti, a přidejte tento vektor do u.

Je velmi důležité si uvědomit, že odčítání vektorů není komutativní, to znamená, že pořadí vektorů nemění výsledek, proto:

nebo - proti ≠ proti - nebo

Grafický postup lze provést pomocí kterékoli z těchto metod, jejichž kroky vysvětlíme níže:

-Metoda trojúhelníku.

-Metoda rovnoběžníku.

Rejstřík článků

• 1 Grafická metoda odčítání vektorů
  • 1.1 Metoda trojúhelníku
  • 1.2 Metoda rovnoběžníku
• 2 Příklady vektorového odčítání
  • 2.1 - Příklad 1
  • 2.2 - Příklad 2
• 3 Cvičení vyřešeno
  • 3.1 Řešení
• 4 Odkazy

Metoda odčítání grafických vektorů

Metoda trojúhelníku

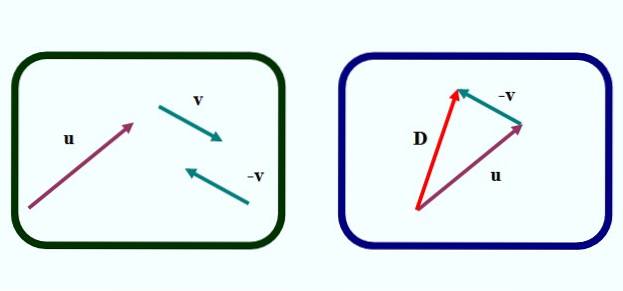
Na obrázku 1 máme první z metod, jak graficky odečíst dva vektory. Je to o trojúhelníková metoda, protože obrazec, který je vytvořen vytvořením vektorů, je trojúhelník, jak vidíme na levém obrázku.

Chcete-li odečíst nebo - proti postupujeme následovně:

-Nakreslete vektor -proti z vektoru proti, překladem pravítkem a čtvercem, ale změnou směru šipky (obrázek vlevo).

-Přesune se na vektor -proti takovým způsobem, že jeho počátek se shoduje s koncem vektoru nebo (pravý obrázek).

-Dále je nakreslen vektor (červeně na pravém obrázku), který jde od počátku nebo do konce roku proti. Volání D y je vektor rozdílu:

D = nebo - proti

Metoda rovnoběžníku

V metodě rovnoběžníku se vektory, které mají být přidány nebo odečteny, musí shodovat v jejich počátečních bodech. Předpokládejme, že chceme najít nebo - proti S našimi vektory zobrazenými výše jsou kroky k nalezení odčítání vektorů touto metodou následující:

-Určete opačný vektor proti, Co je to -proti, jak je popsáno výše pro trojúhelníkovou metodu.

-Pečlivě překládejte vektory nebo Y -proti takovým způsobem, že se jejich původ shoduje.

-Nyní jsou nakresleny segmentované paralelní čáry počínaje konci každého vektoru. Tvarovaný obrazec je rovnoběžník a ve zvláštních případech, kdy jsou vektory kolmé, vznikne obdélník nebo čtverec..

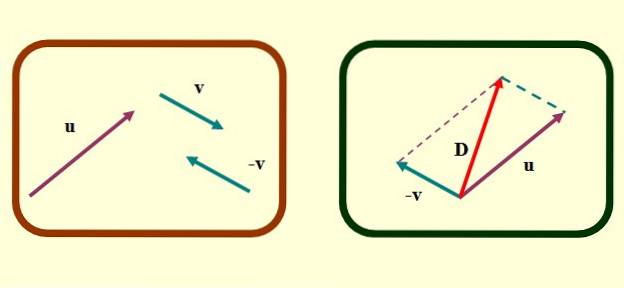
-Nakonec je nakreslen vektor, který začíná společným počátkem nebo Y proti do extrému, kde se protínají segmentované paralelní čáry. Toto je vektor D nebo odčítání.

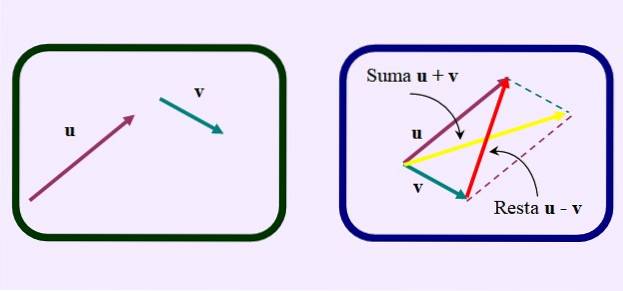
Důležité

Další způsob, jak odečíst, je nakreslit rovnoběžník, jako byste chtěli přidat vektory.

Ale místo kreslení obvyklé úhlopříčky součtu, která jde od společného počátku k průsečíku rovnoběžek, opačná nebo kratší úhlopříčka, jak je vidět na obrázku:

Příklady vektorového odčítání

- Příklad 1

Loď pluje po řece a dělá to v opačném směru než je proud. Pozorovatel na zemi pozoruje, že rychlost lodi je snížena v důsledku působení proudu.

Rychlost je vektor a v tomto příkladu rychlost lodi směřuje jedním směrem a rychlost proudu má stejný směr a opačný směr. Čistá rychlost lodi je součtem obou vektorů.

Například pokud nástroje lodi naznačují, že se pohybuje rychlostí v '= + 40 km / ha pozorovatel na břehu měří, že se loď pohybuje rychlostí v = + 30 km / h. Protože v = v '+ Vc, kde Vc je rychlost proudu, která se vypočítá odečtením rychlostí v a v': Vc = v - v '= 30 km / h - 40 km / h = -10 km / h.

- Příklad 2

V kinematice máme důležité vektory, které popisují změny:

-Ofset pro změny polohy.

-Průměrná rychlost pro kvantifikaci toho, jak rychle se pozice v čase mění.

-Zrychlení, pro změny rychlosti v závislosti na čase.

Vektor posunutí

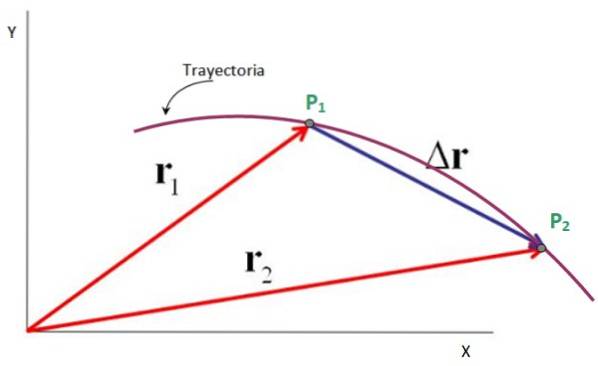
Vektor posunutí popisuje změnu polohy, kterou tělo zažívá během svého pohybu.

Podívejme se například na částici, která popisuje rovinnou cestu zobrazenou na obrázku, ve které prochází z bodu P₁ do bodu P_dva.

Vektory směrované od počátku souřadného systému x-y do těchto bodů jsou polohové vektory r₁ Y r_dva, zatímco vektor posunutí je Δr, to jde od P₁ horní_dva. Je pravda, že:

Δr = r_dva - r₁

Proto je vektor posunutí odečtením mezi vektorem konečné polohy a vektorem počáteční polohy, jak je znázorněno na následujícím obrázku. Jeho jednotkami jsou také jednotky polohy: metry, stopy, míle, centimetry a další..

Střední rychlost a střední vektory zrychlení

Vektor střední rychlosti proti_m je definován jako offset vynásobený inverzí časového intervalu:

Cvičení vyřešeno

Částice, která popisuje kruh, trvá 5 s, než projde z bodu A do bodu B. V bodě A má rychlost proti_NA = 60 km / h směrem k ose x a v bodě B je proti_B = 60 km / h směrem k + y. Určete jeho průměrné zrychlení graficky a analyticky.

Řešení

V grafické podobě jsou směr a směr středního zrychlení určeny:

Na následujícím obrázku je odčítání proti_B - proti_NA, pomocí trojúhelníkové metody, protože průměrné zrychlení na_m je úměrná Δproti. Vytvořený trojúhelník má dvě nohy stejné, a proto každý ostrý vnitřní úhel měří 45 °..

Analyticky, pokud se směr + x shoduje s jednotkovým vektorem i a směr + y s jednotkovým vektorem j, pak:

Δproti = 60 km / h j - 60 km / h i

Vezmeme-li Δt = 5 s, podle informací ve výkazu je střední zrychlení:

na_m = (60 km / h j - 60 km / h i) / 5 s = 12 (j-i) km / (h.s)

Reference

1. Bauer, W. 2011. Fyzika pro inženýrství a vědy. Svazek 1. Mc Graw Hill.
2. Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
3. Figueroa, D. (2005). Série: Fyzika pro vědu a techniku. Svazek 1. Kinematika. Upravil Douglas Figueroa (USB).
4. Giambattista, A. 2010. Fyzika. 2. místo Ed. McGraw Hill.
5. Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14. Vydání Volume 1.
6. Tipler, P. 2006. Fyzika pro vědu a technologii. 5. vyd. Svazek 1. Redakční reverté.