
Důkaz o existenci a jedinečnosti, příklady a cvičení
The Věta o existenci a jedinečnosti stanoví nezbytné a dostatečné podmínky, aby diferenciální rovnice prvního řádu s danou počáteční podmínkou měla řešení a aby toto řešení bylo také jediným.
Věta však neposkytuje žádnou techniku ani indikaci, jak takové řešení najít. Věta o existenci a jedinečnosti je také rozšířena na diferenciální rovnice vyššího řádu s počátečními podmínkami, která je známá jako Cauchyho problém..
Formální prohlášení o teorému o existenci a jedinečnosti je následující:
"Pro diferenciální rovnici y '(x) = f (x, y) s počátečním stavem y (a) = b, existuje alespoň jedno řešení v obdélníkové oblasti roviny XY obsahující k věci (a, b), Ano f (x, y) v tomto regionu je kontinuální. A pokud parciální derivace F ve vztahu k Y: g = ∂f / A je spojitý ve stejné obdélníkové oblasti, pak je řešení jedinečné v sousedství bodu (a, b) obsah v oblasti kontinuity F Y G."
Užitečnost této věty spočívá nejprve ve znalostech, které jsou oblasti roviny XY, ve kterých může řešení existovat, a také ve znalostech, zda je nalezené řešení jediné možné nebo zda existují další..
Všimněte si, že v případě, že podmínka jedinečnosti není splněna, nemůže věta předpovědět, kolik řešení má Cauchyho problém celkem: možná je to jedna, dvě nebo více.
Rejstřík článků
- 1 Důkaz o existenci a jedinečnosti věty
- 2 Příklady
- 2.1 - Příklad 1
- 2.2 - Příklad 2
- 3 Vyřešená cvičení
- 3.1 - Cvičení 1
- 3.2 - Cvičení 2
- 4 Odkazy
Důkaz o existenci a jedinečnosti věty

Pro tuto větu jsou známy dva možné důkazy, jedním z nich je důkaz Charlese Émile Picarda (1856-1941) a druhým je Giuseppe Peano (1858-1932) na základě děl Augustina Louise Cauchyho (1789-1857) ).
Je pozoruhodné, že nejbrilantnější matematické mysli devatenáctého století se podílely na důkazu této věty, takže lze předpokládat, že ani jeden z těchto dvou není jednoduchý.
K formálnímu prokázání věty je nutné nejprve vytvořit řadu pokročilejších matematických konceptů, jako jsou funkce typu Lipschitz, Banachovy prostory, Carathéodoryho věta o existenci a několik dalších, které přesahují rámec článku..
Velká část diferenciálních rovnic, které se ve fyzice zpracovávají, se zabývá spojitými funkcemi v zájmových oblastech, proto se omezíme na ukázání toho, jak je věta aplikována v jednoduchých rovnicích.
Příklady
- Příklad 1
Uvažujme následující diferenciální rovnici s počáteční podmínkou:
y '(x) = - y; s y (1) = 3
Existuje řešení tohoto problému? Je to jediné možné řešení?
Odpovědi
Nejprve se hodnotí existence řešení diferenciální rovnice, která také splňuje počáteční podmínku.
V tomto příkladu f (x, y) = - y podmínka existence vyžaduje vědět, zda f (x, y) je spojitá v oblasti roviny XY který obsahuje bod souřadnic x = 1, y = 3.
Ale f (x, y) = - y je afinní funkce, který je spojitý v doméně reálných čísel a existuje v celém rozsahu reálných čísel.
Proto se dospělo k závěru, že f (x, y) je spojitá v Rdva, věta tedy zaručuje existenci alespoň jednoho řešení.
S tímto vědomím je nutné vyhodnotit, zda je řešení jedinečné, nebo zda je naopak více než jedno. K tomu je nutné vypočítat parciální derivaci F s ohledem na proměnnou Y:
∂f / ∂y = ∂ (-y) / ∂y = -1
Pak g (x, y) = -1 což je konstantní funkce, která je také definována pro všechny Rdva a je to tam také kontinuální. Z toho vyplývá, že věta o existenci a jedinečnosti zaručuje, že tento problém s počáteční hodnotou má jedinečné řešení, i když nám neříká, o co jde..
- Příklad 2
Zvažte následující obyčejnou diferenciální rovnici prvního řádu s počáteční podmínkou:
y '(x) = 2√y; y (0) = 0.
Existuje řešení y (x) pro tento problém? Pokud ano, zjistěte, zda existuje jeden nebo více než jeden.
Odpovědět
Uvažujeme o funkci f (x, y) = 2√y. Funkce F je definováno pouze pro y≥0, protože víme, že zápornému číslu chybí skutečný kořen. Co víc f (x, y) je spojitý v horní polovině roviny Rdva včetně osy X, tak věta o existenci a jedinečnosti zaručuje alespoň jedno řešení v dané oblasti.
Nyní je počáteční podmínka x = 0, y = 0 na okraji oblasti řešení. Pak vezmeme parciální derivaci f (x, y) vzhledem k y:
∂f/ ∂y = 1 / √y
V tomto případě není funkce definována pro y = 0, přesně tam, kde je počáteční podmínka.
Co nám říká věta? Říká nám, že i když víme, že existuje alespoň jedno řešení, horní polovina roviny osy X včetně osy X, protože není splněna podmínka jedinečnosti, neexistuje záruka, že bude existovat jedinečné řešení.
To znamená, že v oblasti spojitosti f (x, y) může existovat jedno nebo více než jedno řešení. A jako vždy, věta nám neříká, čím by mohli být.
Vyřešená cvičení
- Cvičení 1
Vyřešte problém Cauchy v příkladu 1:
y '(x) = - y; s y (1) = 3.
Najděte funkci y (x), která splňuje diferenciální rovnici a počáteční podmínku.
Řešení
V příkladu 1 bylo stanoveno, že tento problém má řešení a je také jedinečný. Chcete-li najít řešení, je třeba si nejprve uvědomit, že se jedná o diferenciální rovnici prvního stupně oddělitelných proměnných, která je napsána následovně:
dy / dx = - y → dy = -y dx
Dělením mezi a v obou členech k oddělení proměnných máme:
dy / y = - dx
Neurčitý integrál se použije u obou členů:
∫ (1 / r) dy = - ∫dx
Řešení neurčitých integrálů, které máme:
ln (y) = -x + C
kde C je integrační konstanta, která je určena počáteční podmínkou:
ln (3) = -1 + C, tj. C = 1 + ln (3)
Dosazením hodnoty C a přeskupením zůstává:
ln (y) - ln (3) = -x + 1
Použití následující vlastnosti logaritmů:
Rozdíl logaritmů je logaritmus kvocientu
Výše uvedený výraz lze přepsat takto:
ln (y / 3) = 1 - x
Exponenciální funkce se základnou e v obou členech se použije k získání:
y / 3 = e(1 - x)
Což odpovídá:
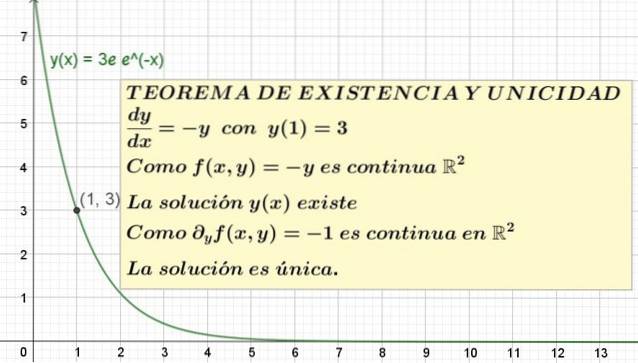
y = 3e e-X
Toto je jedinečné řešení rovnice y '= -y s y (1) = 3. Graf tohoto řešení je znázorněn na obrázku 1.
- Cvičení 2
Najděte dvě řešení problému uvedeného v příkladu 2:
y '(x) = 2√ (y); y (0) = 0.
Řešení
Je to také rovnice oddělitelných proměnných, která, napsaná v diferenciální formě, vypadá takto:
dy / √ (y) = 2 dx
Vezmeme neurčitý integrál v obou členech zůstává:
dva √ (y) = 2 x + C.
Jak víte, že y≥0 v oblasti řešení máme:
y = (x + C)dva
Ale protože musí být splněna počáteční podmínka x = 0, y = 0, pak je konstanta C nulová a zůstane následující řešení:
y (x) = xdva.
Ale toto řešení není jedinečné, funkce y (x) = 0 je také řešením nastoleného problému. Věta o existenci a jedinečnosti aplikovaná na tento problém v příkladu 2 již předpověděla, že může existovat více než jedno řešení.
Reference
- Coddington, hrabě A .; Levinson, Norman (1955), Teorie obyčejných diferenciálních rovnic, New York: McGraw-Hill.
- Encyclopedia of Mathematics. Cauchy-Lipschitzova věta. Obnoveno z: encyclopediaofmath.org
- Lindelöf, Sur l'application de la méthode des aproximations successives aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l'Académie des sciences. Svazek 116, 1894, str. 454-457. Obnoveno z: gallica.bnf.fr.
- Wikipedia. Picardova postupná aproximační metoda. Obnoveno z: es.wikipedia.com
- Wikipedia. Picard-Lindelöfova věta. Obnoveno z: es.wikipedia.com.
- Zill, D. 1986. Elementární diferenciální rovnice s aplikacemi. Prentice Hall.



Zatím žádné komentáře