
Popis Nortonovy věty, aplikace, příklady a cvičení
The Nortonova věta, který se aplikuje na elektrické obvody, stanoví, že lineární obvod se dvěma svorkami a a b lze nahradit úplně rovnocenným, který se skládá ze zdroje proudu zvaného INe zapojen paralelně s odporem RNe.
Řekl proud I.Ne slyšel jsemN Je to ten, který by proudil mezi body a a b, kdyby byly zkratovány. Odpor RN je ekvivalentní odpor mezi svorkami, když se vypnou všechny nezávislé zdroje. Vše, co je řečeno, je uvedeno na obrázku 1.

Černá skříňka na obrázku obsahuje lineární obvod, který má být nahrazen ekvivalentem Norton. Lineární obvod je obvod, ve kterém mají vstup a výstup lineární závislost, jako je například vztah mezi napětím V a stejnosměrným proudem I v ohmickém prvku: V = I.R.
Tento výraz odpovídá Ohmovu zákonu, kde R je odpor, kterým může být také impedance, pokud se jedná o obvod se střídavým proudem.
Nortonovu větu vyvinul elektrotechnik a vynálezce Edward L. Norton (1898-1983), který dlouho pracoval pro Bell Labs..
Rejstřík článků
- 1 Aplikace Nortonovy věty
- 1.1 Vztah mezi větami Norton a Thevenin
- 2 Příklad
- 3 Cvičení vyřešeno
- 4 Odkazy
Aplikace Nortonovy věty
Pokud máte velmi komplikované sítě s mnoha odpory nebo impedancemi a chcete vypočítat napětí mezi kterýmikoli z nich nebo proud, který nimi protéká, Nortonova věta zjednodušuje výpočty, protože jak jsme viděli, síť lze nahradit menší a zvládnutelnější okruh.
Tímto způsobem je Nortonova věta velmi důležitá při navrhování obvodů s více prvky, jakož i při studiu jejich odezvy..
Vztah mezi Nortonovými a Theveninovými větami
Nortonova věta je duálem Theveninovy věty, což znamená, že jsou rovnocenné. Theveninova věta naznačuje, že černý rámeček na obrázku 1 může být nahrazen zdrojem napětí v sérii s odporem, nazývaným Theveninův odpor RČt. To je vyjádřeno na následujícím obrázku:
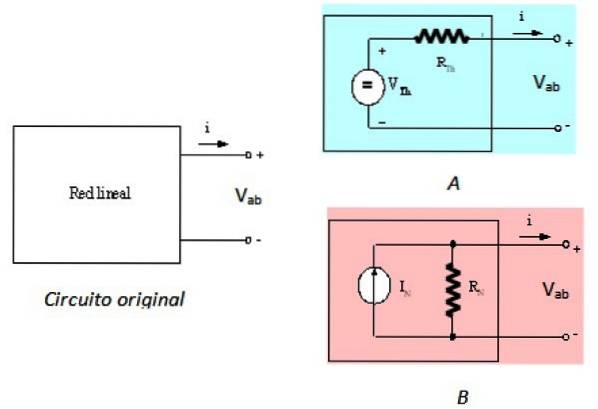
Obvod vlevo je původní obvod, lineární síť v černé skříňce, obvod A vpravo nahoře je ekvivalent Thevenin a obvod B je to ekvivalent Norton, jak je popsáno. Při pohledu ze svorek a a b jsou tyto tři obvody rovnocenné.
Nyní si všimněte, že:
-V původním obvodu je napětí mezi svorkami Vab.
-PROTIab = VČt v okruhu NA
-Nakonec Vab = JáN.RN v okruhu B
Pokud jsou svorky a a b zkratovány ve všech třech obvodech, musí být zajištěno, že napětí a proud mezi těmito body musí být stejné pro všechny tři, protože jsou ekvivalentní. Pak:
-V původním obvodu je proud i.
-Pro obvod A je proud i = VČt / R.Čt, podle Ohmova zákona.
-Nakonec v obvodu B je proud I.N
Proto se dospělo k závěru, že Nortonův a Theveninův odpor mají stejnou hodnotu a že proud je dán:
i = jáN = VČt / R.Čt = VČt / R.N
Příklad
Chcete-li správně použít Nortonovu větu, postupujte následovně:
-Odpojte od sítě část obvodu, pro kterou se nachází ekvivalent Norton.
-Ve zbývajícím obvodu označte svorky a a b.
-Nahraďte zdroje napětí pro zkraty a zdroje proudu pro otevřené obvody, abyste našli ekvivalentní odpor mezi svorkami a a b. To je R.N.
-Vraťte všechny zdroje do jejich původních pozic, zkratujte svorky a a b a najděte proud, který mezi nimi teče. To jsem jáN.
-Nakreslete ekvivalentní obvod Norton podle toho, co je naznačeno na obrázku 1. Zdroj proudu i ekvivalentní odpor jsou paralelní.
Můžete také použít Theveninovu větu k nalezení R.Čt, že už víme, že se rovná RN, pak podle Ohmova zákona najdete IN a pokračujte v kreslení výsledného obvodu.
A teď se podívejme na příklad:
Najděte ekvivalent Norton mezi body A a B následujícího okruhu:
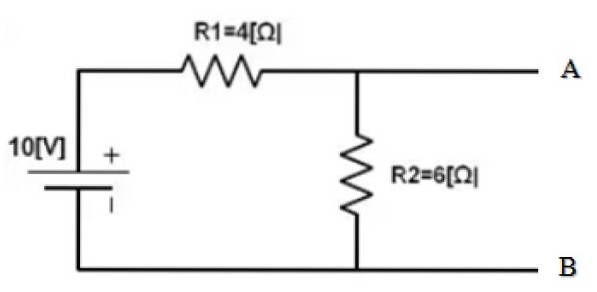
Část obvodu, jehož ekvivalent se nachází, je již izolovaná. A body A a B jsou jasně určeny. Následuje zkratování zdroje 10 V a nalezení ekvivalentního odporu získaného obvodu:
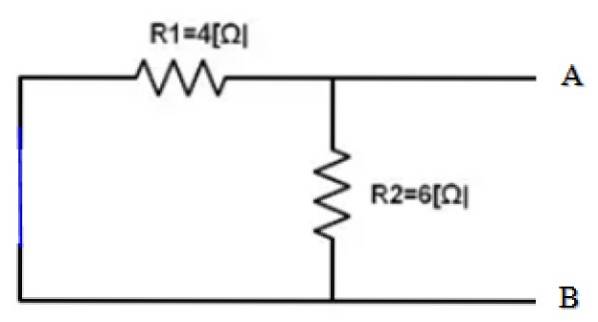
Pohledy z terminálů A a B., oba odpory R1 a R.dva jsou paralelní, proto:
1 / R.ekv = 1 / R.12 = (1/4) + (1/6) Ω-1 = 5/12 Ω-1 → R.ekv = 12/5 Ω = 2,4 Ω
Poté se zdroj vrátí na své místo a body A a B jsou zkratovány, aby se našel proud, který tam cirkuluje, to bude IN. V tom případě:
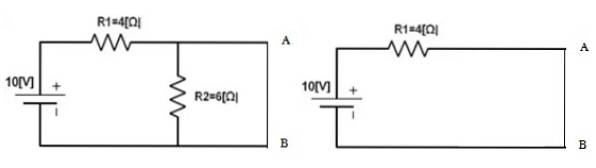
JáN = 10 V / 4 Ω = 2,5 A
Nortonův ekvivalent
Nakonec je ekvivalent Norton nakreslen s nalezenými hodnotami:
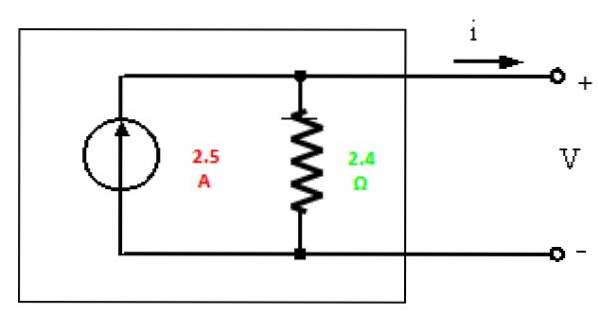
Cvičení vyřešeno
V obvodu následujícího obrázku:
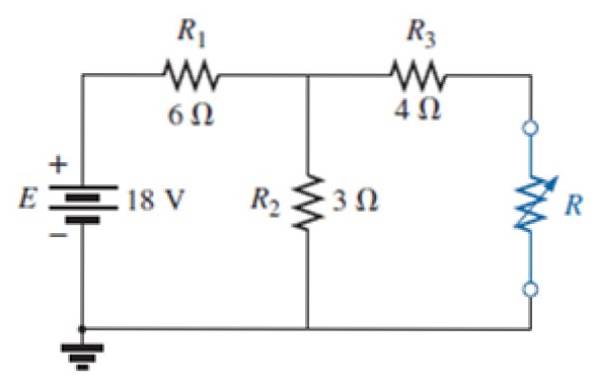
a) Najděte ekvivalentní obvod Norton externí sítě k modrému rezistoru.
b) Najděte také ekvivalent Thévenin.
Řešení
Podle výše uvedených kroků musí být zdroj zkratován:
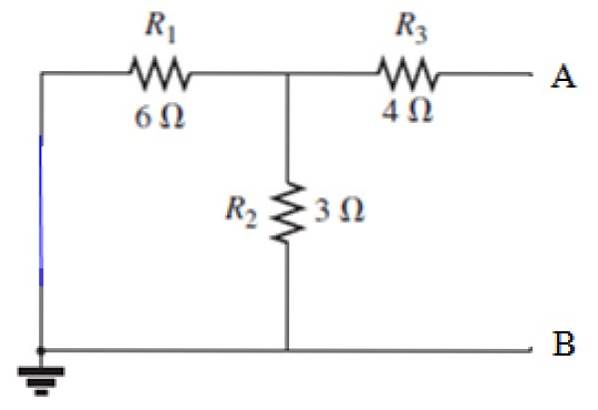
Výpočet RN
Pohled ze svorek A a B, odpor R3 je v sérii s rovnoběžkou tvořenou odpory R1 a R.dva, Pojďme nejprve vypočítat ekvivalentní odpor této paralely:
1 / R.12 = (1/6) + (1/3) Ω-1 = 1/2 Ω-1 → R.ekv = 2/1 Ω = 2Ω
A pak je tato paralela v sérii s R.3, takže ekvivalentní odpor je:
Rekv = 2 Ω + 4 Ω = 6 Ω
Toto je hodnota obou R.N jako z R.Čt, jak bylo vysvětleno dříve.
Výpočet IN
Svorky A a B jsou poté zkratovány a zdroj je vrácen na své místo:
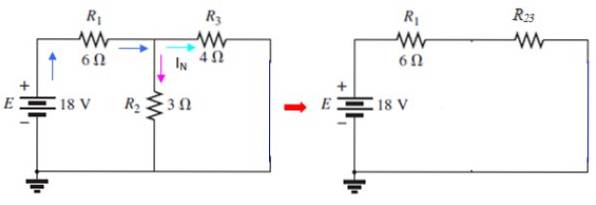
Proud skrz I3 je aktuální IN které lze určit pomocí metody mřížky nebo pomocí řady a paralelně. V tomto obvodu Rdva a R.3 jsou paralelní:
1 / R.2. 3 = (1/3) + (1/4) Ω-1 = 7/12 Ω-1 → R.2. 3 = 12/7 Ω
Odpor R1 je v sérii s touto paralelní, pak:
R123 = 6 + (12/7) Ω = 54/7 Ω
Proud opouštějící zdroj (modrá barva) se vypočítá pomocí Ohmova zákona:
V = I. R → I = V / R = 18 V / (54/7 Ω) = 7/3 A
Tento proud je rozdělen do dvou částí: jedné, která prochází R.dva a další, která protíná R3. Proud přes paralelní R2. 3 je to stejné, co prochází R.1, jak je vidět v meziobvodu na obrázku. Napětí je:
PROTI2. 3 = I.R.2. 3 = (7/3) A. (12/7) Ω = 4 V.
Oba odpory Rdva a R.3 jsou na tomto napětí, protože jsou paralelní, proto:
Já3 = V2. 3 / R.3 = 4 V / 4 Ω = 1 A
Již máme hledaný aktuální Norton, protože jak jsem již řekl dříve3 = JáN, pak:
JáN = 1 A
Nortonův ekvivalent
Všechno je připraveno nakreslit Nortonův ekvivalent tohoto okruhu mezi body A a B:
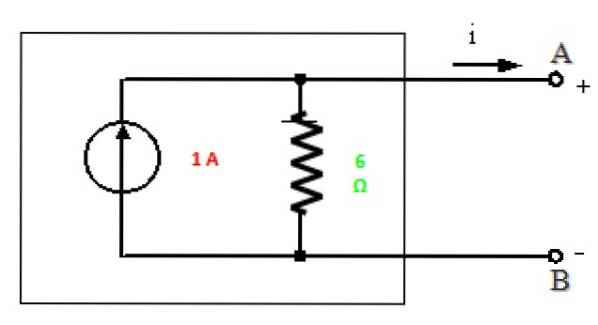
Řešení b
Nalezení ekvivalentu Thévenin je velmi jednoduché, protože RČt = R.N= 6 Ω a jak je vysvětleno v předchozích částech:
PROTIČt = JáN. RN = 1 A. 6 Ω = 6 V
Ekvivalentní okruh Thévenin je:
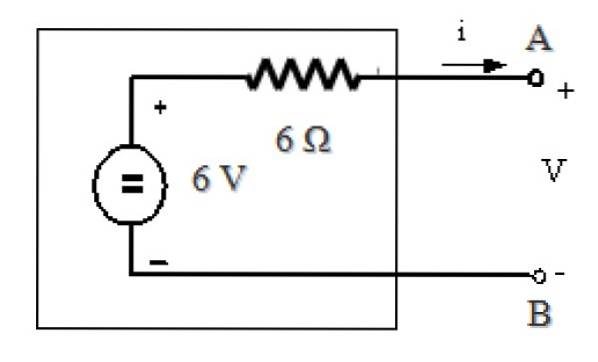
Reference
- Alexander, C. 2006. Základy elektrických obvodů. 3. místo Edice. Mc Graw Hill.
- Boylestad, R. 2011. Úvod do analýzy obvodů. 2. místo Edice. Pearson.
- Dorf, R. 2006. Úvod do elektrických obvodů. 7. Edice. John Wiley & Sons.
- Edminister, J. 1996. Elektrické obvody. Série Schaum. 3. místo Edice. Mc Graw Hill.
- Wikipedia. Nortonova věta. Obnoveno z: es.wikipedia.org.



Zatím žádné komentáře