
Vzorce, rovnice, příklady pro vertikální záběr
The vertikální záběr Jedná se o pohyb, který probíhá působením silového pole, obvykle gravitačního, a může být stoupající nebo klesající. To je také známé pod jménem vertikální spuštění.
Nejbezprostřednějším příkladem je házení (nebo dáváte-li dolů) míč rukou, samozřejmě, ujistěte se, že to děláte ve svislém směru. Bez ohledu na odpor vzduchu se pohyb, který míč sleduje, dokonale hodí k modelu MRUV (Uniformly Varied Rectilinear Motion)..

Vertikální výstřel je pohyb široce studovaný v úvodních kurzech fyziky, protože je ukázkou pohyb v jedné dimenzi, velmi jednoduchý a užitečný model.
Tento model lze použít nejen ke studiu kinematiky objektů působením gravitace, ale také, jak bude vidět později, popisuje pohyb částic uprostřed jednotného elektrického pole..
Rejstřík článků
- 1 Vzorce a rovnice
- 1.1 Rovnice vertikálního hodu
- 2 Příklady
- 2.1 Pracoval příklad 1
- 2.2 Pracoval příklad 2
- 3 Odkazy
Vzorce a rovnice
První věcí, kterou je třeba, je souřadný systém, který označuje počátek a označuje jej písmenem, což je v případě svislých pohybů písmeno „Y".
Poté je vybrán kladný směr +Y, což je obvykle nahoru a smysl -Y který se obvykle sundává (viz obrázek 2). To vše, pokud řešitel problému nerozhodne jinak, protože další možností je vzít směr pohybu jako pozitivní, ať už je jakýkoli..
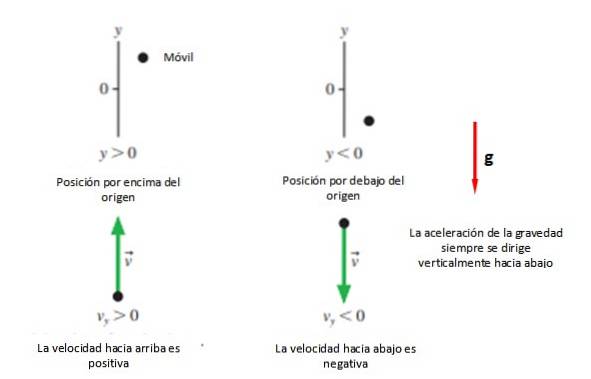
V každém případě se doporučuje, aby se počátek shodoval s bodem spuštění. Ynebo, protože tímto způsobem jsou rovnice zjednodušené, i když můžete zaujmout libovolnou pozici, kterou chcete začít studovat pohyb.
Rovnice vertikálního hodu
Jakmile jsme vytvořili souřadný systém a počátek, jdeme k rovnicím. Veličiny, které popisují pohyb, jsou:
-Počáteční rychlost protinebo
-Akcelerace na
-Rychlost proti
-Počáteční pozice Xnebo
-Pozice X
-Přemístění DX
-Počasí t
Vše kromě času jsou vektory, ale protože se jedná o jednorozměrný pohyb s určitým směrem, je důležité použít znaménka + nebo - k označení, kam se bude daná velikost pohybovat. V případě vertikálního ponoru gravitace vždy klesá dolů a pokud není uvedeno jinak, je jí přiřazeno znaménko -.
Následují rovnice přizpůsobené pro svislý ponor a nahrazují se slovy „X" pro "Y„Y“na" pro "G“. Navíc bude najednou zahrnuto znaménko (-) odpovídající gravitaci směřující dolů:
1) Pozice: y = ynebo + protinebo.t - ½ g.t.dva
2) Rychlost: v = vnebo - g.t.
3) Rychlost jako funkce posunutí ΔY: protidva = vnebodva - 2 g. ΔY
Příklady
Níže jsou uvedeny příklady aplikací pro vertikální fotografování. Při jeho řešení je třeba vzít v úvahu následující:
-"G„Má konstantní hodnotu, která je v průměru 9,8 m / sdva nebo asi 10 m / sdva pokud je to upřednostňováno pro usnadnění výpočtů, když není vyžadována příliš velká přesnost.
-Když protinebo dobře 0, tyto rovnice se redukují na rovnice volný pád.
-Pokud je start vzhůru, musí mít objekt počáteční rychlost, která mu umožňuje pohyb. Jakmile je objekt v pohybu, dosáhne maximální výšky, která bude záviset na tom, jak velká je počáteční rychlost. Samozřejmě čím vyšší nadmořská výška, tím více času stráví mobil ve vzduchu.
-Objekt se vrací do výchozího bodu se stejnou rychlostí, s jakou byl vržen, ale rychlost je směrována dolů.
-Při vertikálním spuštění směrem dolů platí, že čím vyšší je počáteční rychlost, tím dříve objekt dopadne na zem. Zde se nastavuje ujetá vzdálenost podle výšky vybrané pro start.
-Při svislém hodu nahoru se čas, který mobilnímu zařízení dosáhne maximální výšky, vypočítá provedením v = 0 v rovnici 2) předchozí části. To je maximální čas tmax:
0 = vnebo - G. tmax ⇒ tmax = vnebo / g
-The maximální výška Ymax je odstraněno z rovnice 3) předchozí části stejným způsobem v = 0:
0 = vnebodva - 2 g. Δy ⇒ 0 = vnebodva - 2 g. (Ymax - Ynebo) ⇒ amax = anebo + protinebodva / 2 g
Ano Ynebo = 0, Snižuje se na:
Ymax = vnebodva / 2 g
Pracoval příklad 1
Míč je vrhán svisle nahoru pomocí vnebo = 14 m / s, z vrcholu 18 m vysoké budovy. Míč může pokračovat v cestě dolů na chodník. Vypočítat:
a) Maximální výška dosažená míčem vzhledem k zemi.
b) čas, kdy byl ve vzduchu (doba letu).
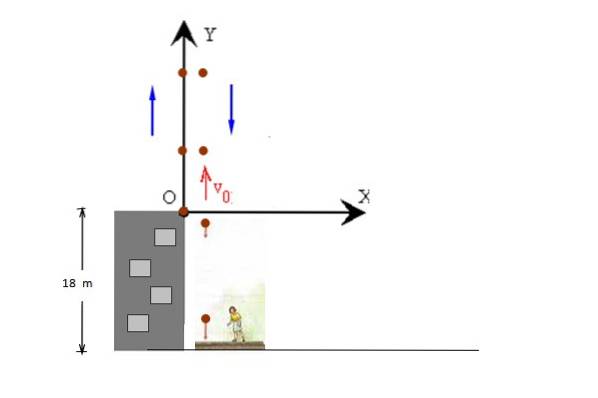
Řešení
Obrázek ukazuje pohyby zvedání a spouštění míče samostatně kvůli jasnosti, ale oba se vyskytují ve stejné linii. Počáteční poloha je zaujata na y = 0, takže konečná poloha je y = - 18 m.
a) Maximální výška měřená od střechy budovy je Ymax = vnebodva / 2 g a z tvrzení můžeme vyčíst, že počáteční rychlost je +14 m / s, pak:
Ymax = (14 m / s)dva / 2 x 9,8 m / sdva = 10 m (Co se týče střechy)
Hmax = 10 m + 18 m = 28 m (Ohledně chodníku).
b) Najít celkový čas nebo doba letu míč vydrží ve vzduchu, použije se rovnice y = ynebo + protinebo.t - ½ g.t.dva, s následujícími hodnotami a znaky:
y = - 18 m
Ynebo = 0 m
protinebo = +14 m / s
Střídání:
- 18 = 14.t - ½ 9.8 .tdva
- 4,9 tdva+14. t + 18 = 0
4,9 tdva-14. t - 18 = 0
Jedná se o rovnici druhého stupně, kterou lze snadno vyřešit pomocí vědecké kalkulačky nebo pomocí řešiče. Řešení jsou: 3,82 a -0,96. Negativní řešení je zahozeno, protože je to doba, postrádá fyzický smysl.
Doba letu míče je 3,82 sekundy.
Pracoval příklad 2
Kladně nabitá částice s q = +1,2 milicoulombs (mC) a hmotnost m = 2,3 x 10 -10 Kg se promítá svisle nahoru, počínaje pozicí znázorněnou na obrázku a počáteční rychlostí protinebo = 30 km / s.
Mezi nabitými deskami je elektrické pole A rovnoměrné, směrované svisle dolů a s velikostí 780 N / C. Pokud je vzdálenost mezi deskami 18 cm, dojde ke kolizi částic s horní deskou? Zanedbejte gravitační přitažlivost částice, protože je extrémně lehká.
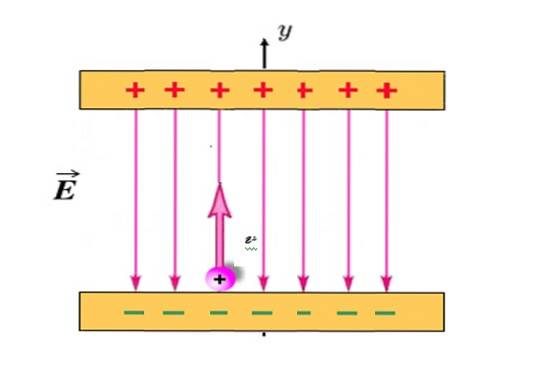
Řešení
V tomto problému elektrické pole A je ten, který produkuje sílu F a následné zrychlení. Při kladném nabití je částice vždy přitahována ke spodní desce, ale když je promítnuta svisle nahoru, dosáhne maximální výšky a poté se vrátí na spodní desku, stejně jako koule v předchozích příkladech..
Podle definice elektrického pole:
E = F / q = m.a / q ⇒ a = q.E / m
Tuto ekvivalenci musíte použít před nahrazením hodnot:
1 mC = 1 x 10-3 C
Zrychlení je tedy:
a = 1,2 x 10-3 x 780 / 2,3 x 10 -10slečnadva = 4,07 x 109 slečnadva
Pro maximální výšku se použije vzorec z předchozí části, ale místo „G„Tato hodnota zrychlení se používá:
Ymax = vnebodva / 2a = (30 000 m / s)dva/ 2 x 4,07 x 109 slečnadva = 0,11 m = 11 cm
Nesrazí se s horní deskou, protože je 18 cm od počátečního bodu a částice dosahuje pouze 11 cm.
Reference
- Kirkpatrick, L. 2007. Fyzika: Pohled na svět. 6ta Zkrácené vydání. Cengage Learning. 23 - 27.
- Rex, A. 2011. Základy fyziky. Pearson. 33 - 36
- Sears, Zemansky. 2016. Univerzitní fyzika s moderní fyzikou. 14th. Vydání 1. 50 - 53.
- Serway, R., Vulle, C. 2011. Základy fyziky. 9na Ed. Cengage Learning. 43 - 55.
- Wilson, J. 2011. Fyzika 10. Pearsonovo vzdělávání. 133 - 149.



Zatím žádné komentáře