Koncept lineární variace, příklady, řešené cvičení

The lineární variace nastává mezi dvěma fyzickými veličinami, když graf, který je představuje, je přímka. Je to ekvivalentní tvrzení, že proměnné jsou v lineární závislosti, a to tak, že pokud jednu z nich nazýváme „y“ a druhou „x“, budou spojeny pomocí matematického výrazu:

y = mx + b

V tomto vzorci jsou m a b reálná čísla. Hodnota m představuje sklon nebo sklon přímky - která je vždy konstantní - a b je řez přímky se svislou osou.

Každý jev, který reaguje na lineární variaci, má pro proměnné různá jména, jak uvidíme v následujících příkladech. Matematická forma rovnice je však stejná.

Experimentálně lze určit, zda existuje lineární vztah mezi dvěma veličinami, měřením dvojic hodnot (x, y).

Takto získané body jsou vyneseny na milimetrový papír a je pozorováno, zda mají lineární trend, tj. Jestli existuje čára, která adekvátně odpovídá experimentálním datům.

V prvním případě lze tuto čáru nakreslit vizuálně, ale pomocí a lineární regrese lze analyticky najít hodnoty mab přímky, které nejlépe vyhovují experimentálním bodům.

Rejstřík článků

• 1 Příklady lineární variace
  • 1,1 Rychlost v přímočarém pohybu rovnoměrně měněna
  • 1.2 Tepelná roztažnost
  • 1.3 Poloha mobilního telefonu s konstantní rychlostí
  • 1.4 Výška osoby
  • 1.5 Teplotní stupnice
  • 1.6 Tlak a hloubka
• 2 Cvičení vyřešeno
  • 2.1 Náklady na řízení
• 3 Odkazy

Příklady lineární variace

Existuje mnoho přírodních jevů a také vztahy mezi standardy měření, které jsou způsobeny lineární variací, například:

Rychlost v přímočarém pohybu se rovnoměrně měnila

Rychlost jako funkce času v (t) mobilního telefonu pohybujícího se po přímce s konstantním zrychlením a a počáteční rychlosti v_nebo  odlišné od 0. Tento pohyb je známý jako rovnoměrně změněný přímočarý pohyb a rovnice pro rychlost je:

v (t) = v_nebo + na

Teplotní roztažnost

Dalším přírodním jevem, jehož variace je lineární, je zvětšení délky, které tyč nebo drát zažívají při zahřívání..

Když se teplota jakéhokoli objektu zvýší, zvýší se také jeho rozměry a toto zvýšení závisí na změně teploty ΔT a veličině zvané koeficient lineární roztažnosti označeno řeckým písmenem α:

L = L_nebo + α ΔT

V tomto výrazu L je konečná délka objektu a L_nebo je jeho počáteční délka.

Poloha mobilního telefonu s konstantní rychlostí

Mobil s rychlost konstanta se vždy pohybuje po přímce. Pokud je přímka vodorovná osa x, je poloha x (t) v kterémkoli okamžiku dána vztahem:

x (t) = x_nebo + vt

Kde x_nebo je počáteční poloha, v je rychlost at je čas. Tímto způsobem se říká, že poloha x se lineárně mění s časem t.

Výška osoby

Lékaři a antropologové mohou odhadnout výšku člověka měřením délky stehenní kosti..

Čím vyšší je člověk, tím delší jsou nohy, takže existují lineární modely pro predikci výšky dospělého člověka H (v palcích), pokud je známa délka L (také v palcích) jeho stehenní kosti, podle rovnice:

H = 1,880⋅L + 32,010

Teplotní stupnice

K měření teploty se denně používají stupnice Celsia a Fahrenheita. Tato poslední stupnice se běžně používá v anglicky mluvících zemích. Od jednoho k druhému existuje rovnocennost:

F = (9/5) C + 32

Kde F je teplota ve stupních Fahrenheita a C je teplota ve stupních Celsia.

Tlak a hloubka

Absolutní tlak P v nestlačitelné tekutině, jako je voda, jejíž konstantní hustota je ρ, se mění v závislosti na hloubce h jako:

P = P_nebo + ρgh

Kde P_nebo je tlak na volném povrchu kapaliny. Pokud je kapalina v nádobě otevřené do atmosféry, je tento tlak jednoduše atmosférickým tlakem P_bankomat, schopnost psát poté:

P = P_bankomat + ρgh

Atmosférický tlak na úrovni moře je přibližně 101 kPa. Tento vztah mezi P a h znamená, že tlak roste lineárně s hloubkou..

Cvičení vyřešeno

Řidičské náklady

Měsíční náklady C na řízení automobilu zahrnují fixní měsíční náklady C_nebo plus náklady na ujeté kilometry nebo počet ujetých kilometrů každý měsíc. Řidič poznamenává, že v daném měsíci byly náklady na řízení 380 $ za 480 mil a další měsíc to bylo 460 $ za 800 mil.

Nechť d je počet kilometrů ujetých řidičem za měsíc, s poskytnutými údaji, najděte:

a) Lineární variace mezi C a d.

b) Kolik by stálo za měsíc řídit auto na cestě dlouhé 1 500 mil?

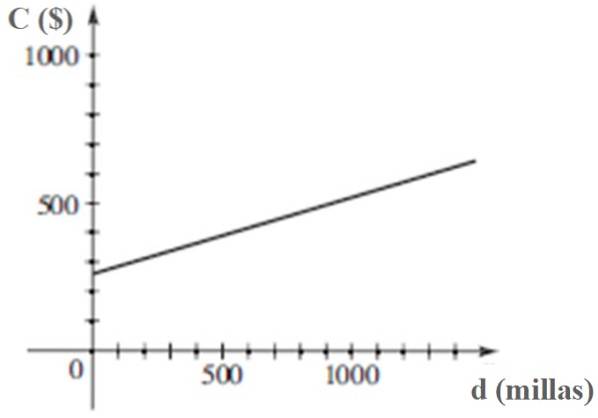
c) Graf C versus d.

Řešení

Předpokládejme, že proměnné mají vztah daný:

C = C_nebo + Inzerát

Kde A a C._nebo jsou konstanty, které se mají určit. A je sklon přímky, která graficky představuje vztah mezi C a d. Co je řez se svislou osou, pevné měsíční náklady, které musí řidič zaplatit za pouhou skutečnost, že má auto k dispozici. To může zahrnovat například náklady na údržbu a daně.

Pro jednoznačné určení přímky je nutné znát její sklon. K tomu máme body:

P₁: 480 mil, 380 $

P_dva: 800 mil, 460 $

Tyto body souřadnic (d, C) nebo (vzdálenost, cena) jsou analogické bodům souřadnic (x, y) kartézské roviny, jejich změny se změní. Sklon A přímky je pak dán vztahem:

A = (C._dva - C₁) / (d_dva - d₁)

A = [(460 - 380) $ / (800 - 480) mil] = (1/4) $ / míli

Sklon čáry představuje cenu za míli, například takto:

C = C_nebo + A.d = Co + (1/4) .d

Chcete-li určit cenu základny C._nebo Tato rovnice je převzata a jeden z bodů, o kterých víme, že do ní patří, je nahrazen, například P₁:

380 $ = C._nebo + [(1/4) $ / míle]. 480 mil → 380 $ = C._nebo + 120 $

C_nebo = 260 $

Nyní můžeme formulovat lineární variační model jako:

C = 260 + (1/4) d

Řešení b

Měsíční náklady na cestování 1 500 mil jsou:

C = 260 + (1/4) x 1500 $ = 635 $

Řešení c

Graf C versus d je:

Reference

1. Baldor. 1977. Elementární algebra. Venezuelské kulturní edice.
2. Hoekenga, C. Lineární rovnice ve vědě. Obnoveno z: visionlearning.com.
3. Hoffman, J. Výběr témat matematiky. Svazek 2.
4. Jiménez, R. 2008. Algebra. Hala Prentice.
5. Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Edice. Cengage Learning.
6. Zill, D. 1984. Algebra a trigonometrie. Mcgraw kopec.