The normální vektor je ten, který definuje směr kolmý na uvažovanou geometrickou entitu, kterou může být například křivka, rovina nebo povrch, například.
Jedná se o velmi užitečný koncept při určování polohy pohybující se částice nebo nějakého povrchu ve vesmíru. V následujícím grafu je možné vidět, jaký je normální vektor k libovolné křivce C:
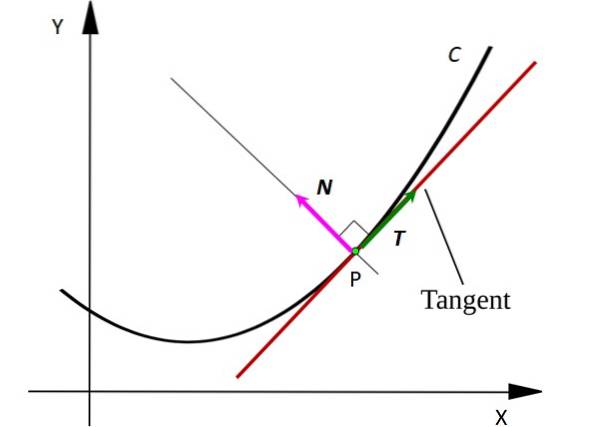
Zvažte bod P na křivce C. Bod může představovat pohybující se částice, která se pohybuje po dráze ve tvaru C. Tečna ke křivce v bodě P je nakreslena červeně..
Všimněte si, že vektor T je tečna k C v každém bodě, zatímco vektor N je kolmá na T y ukazuje do středu imaginární kružnice, jejíž oblouk je segmentem C. Vektory jsou v tištěném textu označeny tučným písmem, aby se odlišily od jiných nevelektrických veličin.
Vektor T vždy označuje, kde se částice pohybuje, proto udává její rychlost. Místo toho vektor N vždy ukazuje ve směru, ve kterém se částice otáčí, tímto způsobem označuje konkávnost křivky C.
Rejstřík článků
Normální vektor nemusí být nutně jednotkový vektor, tj. Vektor, jehož modul je 1, ale pokud ano, je volán normální jednotkový vektor.
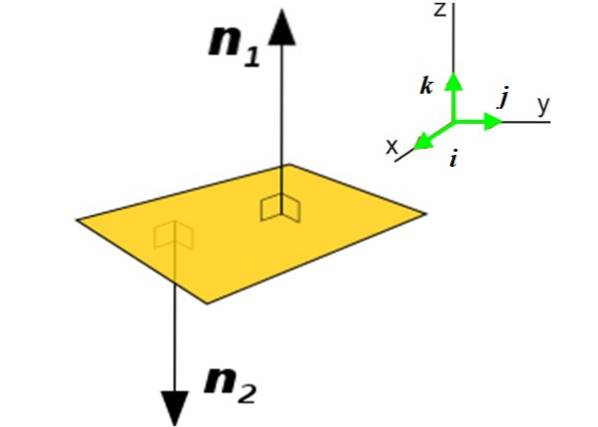
V mnoha aplikacích je nutné znát normální vektor k rovině místo křivky. Tento vektor odhaluje orientaci uvedené roviny v prostoru. Zvažte například letadlo P (žlutá) postavy:
K této rovině existují dva normální vektory: n1 Y ndva. Použití jednoho nebo druhého bude záviset na kontextu, ve kterém se uvedená rovina nachází. Získání normálového vektoru k rovině je velmi jednoduché, pokud znáte jeho rovnici:
ax + by + cz + d = 0, s na, b, C Y d reálná čísla.
Normální vektor k uvedené rovině je dán vztahem:
N = a i + b j + C k
Tady vektor N Vyjadřuje se jednotkovými vektory a je na sebe kolmá i, j Y k, směřující ve třech směrech, které určují prostor X a Z, viz obrázek 2 vpravo.
Velmi jednoduchý postup k nalezení normálního vektoru využívá vlastnosti vektorového produktu mezi dvěma vektory.
Jak je známo, tři různé body, které nejsou kolineární, určují rovinu P. Nyní je možné získat dva vektory nebo Y proti které patří uvedenému letadlu majícímu tyto tři body.
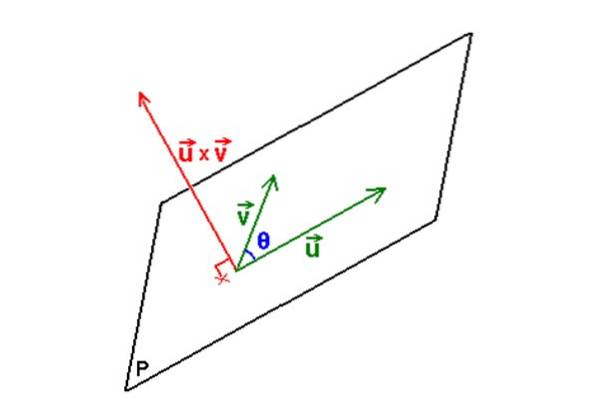
Jakmile máte vektory, vektorový produkt nebo X proti je operace, jejímž výsledkem je zase vektor, který má tu vlastnost, že je kolmý na rovinu určenou pomocí nebo Y proti.
Tento vektor, známý jako, je označen jako N, a z toho bude možné určit rovnici roviny díky rovnici uvedené v předchozí části:
N = nebo X proti
Následující obrázek ilustruje popsaný postup:
Najděte rovnici roviny určenou body A (2,1,3); B (0,1,1); C (4,2,1).
Toto cvičení ilustruje výše popsaný postup. Tím, že má 3 body, je jeden z nich vybrán jako společný počátek dvou vektorů, které patří do roviny definované těmito body. Například bod A je nastaven jako počátek a vektory jsou konstruovány AB Y AC.
Vektor AB je vektor, jehož počátkem je bod A a jehož koncovým bodem je bod B. Souřadnice vektoru AB jsou určeny příslušným odečtením souřadnic B od souřadnic A:
AB = (0-2) i + (1-1) j + (1-3) k = -2i + 0j -dva k
Stejným způsobem postupujeme při hledání vektoru AC:
AC = (4-2) i + (2-1) j + (1-3) k = 2i + j -dva k
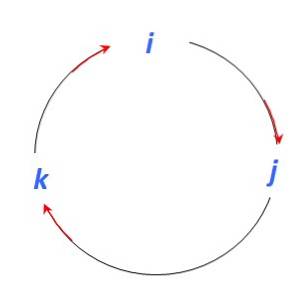
Existuje několik postupů k nalezení vektorového produktu mezi dvěma vektory. Tento příklad používá mnemotechnickou proceduru, která využívá následující obrázek k vyhledání vektorových produktů mezi jednotkovými vektory i, j Y k:
Pro začátek je dobré si uvědomit, že vektorové produkty mezi paralelními vektory jsou nulové, proto:
i X i = 0; j X j = 0; k X k = 0
A protože vektorový produkt je další vektor kolmý na zúčastněné vektory, máme při pohybu ve směru červené šipky:
i X j = k ; j X k = i; k X i = j
Pokud se musíte pohybovat v opačném směru, než je šipka, přidejte znaménko (-):
j X i = - k; k X j = -i; i X k = -j
Celkově je možné s jednotkovými vektory vyrobit 9 vektorových produktů i, j Y k, z toho 3 budou neplatné.
AB X AC = (-2i + 0j -dva k) x (2i + j -dva k) = -4 (i X i) -dva (i X j) +4 (i X k) +0 (j X i) + 0 (j X j) - 0 (j X k) - 4 (k X i) -dva (k X j) + 4 (k X k) = -2k-4j-4j+dvai = 2i -8j-dvak
Vektor N byl určen dříve vypočteným vektorovým produktem:
N = dvai -8j-dvak
Proto a = 2, b = -8, c = -2, hledaná rovina je:
ax + by + cz + d = 0 → 2x-8y-2z + d = 0
Hodnota d. To je snadné, pokud jsou hodnoty kteréhokoli z bodů A, B nebo C, které jsou k dispozici, nahrazeny v rovnici roviny. Volba C například:
x = 4; y = 2; z = 1
Zůstává:
2,4 - 8,2 - 2,1 + d = 0
-10 + d = 0
d = 10
Stručně řečeno, hledaná mapa je:
2x-8y-2z +10 = 0
Zvědavý čtenář se může divit, zda by bylo dosaženo stejného výsledku, kdyby místo toho AB X AC by se rozhodli uskutečnit AC X AB. Odpověď zní ano, rovina určená těmito třemi body je jedinečná a má dva normální vektory, jak je znázorněno na obrázku 2.
Pokud jde o bod vybraný jako počátek vektorů, není problém vybrat kterýkoli z dalších dvou.
Zatím žádné komentáře