
Kolineární vektorový systém a příklady
The kolineární vektory Jsou jedním ze tří typů existujících vektorů. Jedná se o vektory, které jsou ve stejném směru nebo linii působení. To znamená následující: dva nebo více vektorů bude kolineárních, pokud jsou uspořádány do čar, které jsou navzájem rovnoběžné.
Vektor je definován jako veličina aplikovaná na tělo a vyznačuje se tím, že má směr, smysl a měřítko. Vektory lze nalézt v rovině nebo v prostoru a mohou být různých typů: kolineární vektory, souběžné vektory a paralelní vektory.

Rejstřík článků
- 1 Kolineární vektory
- 2 Funkce
- 2.1 Příklad 1
- 2.2 Příklad 2
- 2.3 Příklad 1
- 3 Kolineární vektorový systém
- 3.1 Kolineární vektory s opačnými směry
- 3.2 Kolineární vektory se stejným směrem
- 3.3 Kolineární vektory se stejnými velikostmi a opačnými směry
- 4 Rozdíl mezi kolineárními a souběžnými vektory
- 5 Reference
Kolineární vektory
Vektory jsou kolineární, pokud linie působení jednoho je přesně stejná linie působení všech ostatních vektorů, bez ohledu na velikost a směr každého z vektorů.
Vektory se používají jako reprezentace v různých oblastech, jako je matematika, fyzika, algebra a také v geometrii, kde jsou vektory kolineární, pouze pokud je jejich směr stejný, bez ohledu na to, zda jejich smysl není..
Vlastnosti
- Dva nebo více vektorů je kolineárních, pokud je vztah mezi souřadnicemi stejný.
Příklad 1
Máme vektory m = m_x; m_y a n = n_x; n_y. Jsou kolineární, pokud:
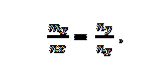
Příklad 2
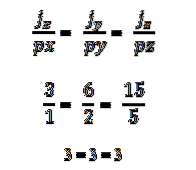
- Dva nebo více vektorů je kolineárních, pokud je vektorový produkt nebo násobení rovné nule (0). Je to proto, že v souřadnicovém systému je každý vektor charakterizován příslušnými souřadnicemi, a pokud jsou navzájem úměrné, vektory budou kolineární. To je vyjádřeno následujícím způsobem:
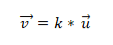
Příklad 1
Máme vektory a = (10, 5) a b = (6, 3). K určení, zda jsou kolineární, je použita teorie determinantů, která stanoví rovnost křížových produktů. Musíte tedy:
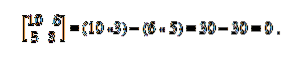
Kolineární vektorový systém
Kolineární vektory jsou graficky znázorněny pomocí jejich směru a smyslu - s přihlédnutím k tomu, že musí projít bodem aplikace - a modulu, což je určité měřítko nebo délka..
Systém kolineárních vektorů je vytvořen, když dva nebo více vektorů působí na objekt nebo tělo, což představuje sílu a působí ve stejném směru..
Například pokud na tělo působí dvě kolineární síly, výslednice z nich bude záviset pouze na směru, ve kterém působí. Existují tři případy, které jsou:
Kolineární vektory s opačnými směry
Výsledek dvou kolineárních vektorů se rovná součtu těchto:
R = ∑ F = F1 + Fdva.
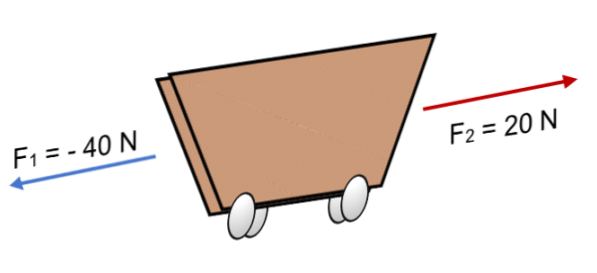
Příklad
Pokud dvě síly F působí na vozík1 = 40 N a Fdva = 20 N v opačném směru (jak je znázorněno na obrázku), výsledek je:
R = ∑ F = (- 40 N) + 20 N..
R = - 20 N..
Kolineární vektory se stejným významem
Velikost výsledné síly se bude rovnat součtu kolineárních vektorů:
R = ∑ F = F1 + Fdva.
Příklad
Pokud dvě síly F působí na vozík1 = 35 N a Fdva = 55 N ve stejném směru (jak je znázorněno na obrázku), výsledek je:
R = ∑ F = 35 N + 55 N..
R = 90 N.
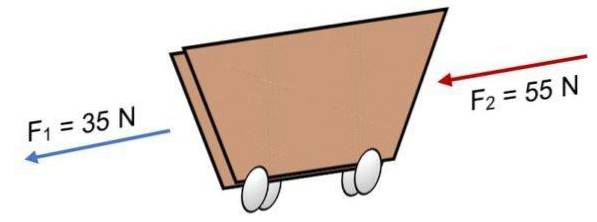
Kladný výsledek znamená, že kolineární vektory působí vlevo.
Kolineární vektory se stejnými velikostmi a opačnými směry
Výsledek dvou kolineárních vektorů se bude rovnat součtu kolineárních vektorů:
R = ∑ F = F1 + Fdva.
Protože síly mají stejnou velikost, ale v opačném směru - to znamená, že jedna bude kladná a druhá záporná -, když se tyto dvě síly sčítají, výslednice se bude rovnat nule..
Příklad
Pokud dvě síly F působí na vozík1 = -7 N a Fdva = 7 N, které mají stejnou velikost, ale v opačném směru (jak je znázorněno na obrázku), je výsledek:
R = ∑ F = (-7 N) + 7N.
R = 0.
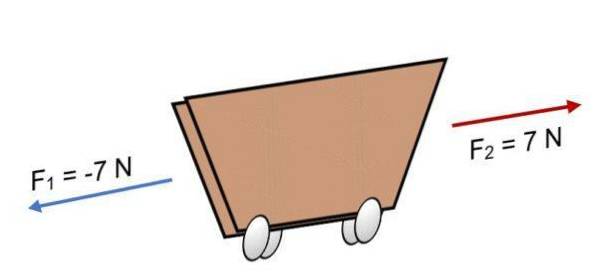
Vzhledem k tomu, že výslednice je rovna 0, znamená to, že vektory se navzájem vyrovnávají, a proto je tělo v rovnováze nebo v klidu (nebude se pohybovat).
Rozdíl mezi kolineárními a souběžnými vektory
Kolineární vektory se vyznačují tím, že mají stejný směr ve stejné linii, nebo proto, že jsou rovnoběžné s linií; to znamená, že jsou vektory vektoru paralelních linií.
Souběžné vektory jsou definovány, protože jsou v různých liniích akce, které se protínají v jednom bodě..
Jinými slovy, mají stejný bod původu nebo příjezdu - bez ohledu na jejich modul, směr nebo směr - tvořící úhel mezi nimi..
Souběžné vektorové systémy jsou řešeny matematickými nebo grafickými metodami, kterými jsou metoda rovnoběžníku sil a metoda mnohoúhelníku sil. Prostřednictvím nich bude určena hodnota výsledného vektoru, který označuje směr, kterým se bude tělo pohybovat.
V zásadě je hlavním rozdílem mezi kolineárními a souběžnými vektory akční linie, ve které působí: kolineární působí ve stejné linii, zatímco souběžné v různých.
To znamená, že kolineární vektory působí v jediné rovině, „X“ nebo „Y“; a souběžné působí v obou rovinách, počínaje od stejného bodu.
Kolineární vektory se v bodě nesetkávají, jako to dělají souběžné vektory, protože jsou navzájem paralelní.
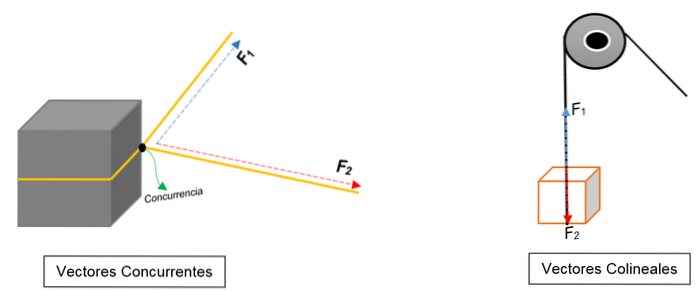
Na levém obrázku vidíte blok. Je svázána provazem a uzel ji rozděluje na dvě části; při tažení směrem k různé orientaci a s různými silami se blok bude pohybovat stejným směrem.
Jsou reprezentovány dva vektory, které se shodují v bodě (bloku), bez ohledu na jejich modul, směr nebo směr.
Na druhé straně je na pravém obrázku kladka, která zvedá krabici. Lano představuje linii akce; když je tažen, působí na něj dvě síly (vektory): tahová síla (když je blok zvednut) a další síla, která vyvíjí váhu bloku. Oba mají stejný směr, ale v opačných směrech; v jednom bodě se neshodují.
Reference
- Estalella, J. J. (1988). Vektorová analýza. Hlasitost 1.
- Gupta, A. (s.f.). Tata McGraw-Hill Education.
- Jin Ho Kwak, S. H. (2015). Lineární algebra. Springer Science & Business Media.
- Montiel, H. P. (2000). Physics 1 for Technological Baccalaureate. Grupo Editorial Patria.
- Santiago Burbano de Ercilla, C. G. (2003). Obecná fyzika. Redakční Tebar.
- Sinha, K. (s.f.). Učebnice matematiky XII, svazek 2. Publikace Rastogi.



Zatím žádné komentáře